EJERCICIOS
1) Hallar "x" en:
2,5 (2) 1,5
3,8 (4) 4,2
$\frac{1}{4}$ (x) 1,75
a) 0 b) 1 c) 2 d) 3
Resolución:
Para obtener el término del medio, buscamos la relación entre términos extremos. observamos en la 1ª y 2ª fila se trata de una suma y el resultado obtenido lo dividimos para 2.
Aplicamos la ley de formación en la 3ª fila para hallar el valor de "x"
2,5 + 1,5 = 4 $ \div $ 2 = 2
3,8 + 4,2 = 8 $ \div $ 2 = 4
0,25 + 1,75 = 2 $ \div $ 2 = 1
x = 1
La respuesta es b.
2) Hallar "b" en:
3,5 7 0,5
7,2 8 0,9
7,5 5 b
a) $\frac{1}{2}$ b) $\frac{1}{4}$ c) $\frac{2}{3}$ d) $\frac{3}{2}$
Resolución:
Buscamos la relación y encontramos en la 1ª fila.
En la 2ª fila se dan las mismas relaciones.
Aplicamos la relación en la 3ª fila
3,5 $\div $ 7 = 0,5
7,2 $\div $ 8 = 0,9
7,5 $\div $ 5 = b
b = 1,5 = $\frac{3}{2}$
La respuesta es d.
3) ¿Qué número falta?
a) $\frac{1}{9}$ b) $\frac{1}{6}$ c) $\frac{1}{3}$ d) $\frac{1}{27}$
Resolución:
Buscamos una relación entre los números que están colocados unos frente al otro como: 2 y 4, el número menor se multiplica por si mismo, se obtiene el número opuesto.
$\frac{1}{2}$ y $\frac{1}{4}$ $\Rightarrow$ $\frac{1}{2}$ $\bullet \; \; \frac{1}{2}$ = $\frac{1}{4}$
2 y 4 $\Rightarrow$ 2 $\bullet$ 2 = 4
$\frac{1}{5}$ y $\frac{1}{25}$ $\Rightarrow$ $\frac{1}{5}$ $\bullet \; \; \frac{1}{5}$ = $\frac{1}{25}$
$\frac{1}{3}$ y x $\Rightarrow$ $\frac{1}{3}$ $\bullet \; \; \frac{1}{3}$ = $\frac{1}{9}$
x = $\frac{1}{9}$
La respuesta es a.
4) ¿Qué número falta?
a) $\frac{1}{8}$ b) 4 c) $\frac{1}{4}$ d) $\frac{1}{3}$
Resolución:
Vemos que relación se cumple en las figuras.
Observamos que en la primera figura se cumple:
$\frac{1}{8}$ $\bullet \; 4$ $\Rightarrow$ $\frac{1}{8}$ $\bullet \; 2^{2}$ = $\frac{1}{2}$
Comprobamos la relación en la segunda figura:
$\frac{1}{27}$ $\bullet \; 9$ $\Rightarrow$ $\frac{1}{8}$ $\bullet \; 3^{2}$ = $\frac{1}{3}$
Se observa que la secuencia es $2^{2}$, $3^{2}$ y continuaría el número $4^{2}$ para obtener el valor de "x".
Aplicamos la relación en la tercera figura:
$\frac{1}{64}$ $\bullet \; 16$ $\Rightarrow$ $\frac{1}{8}$ $\bullet \; 4^{2}$ = $\frac{1}{4}$
La respuesta es c.
5) Distribuya en un cuadro mágico los números 0,2; 0,6; 0,4; 1,8; 1,4; 1,6; 1; 1,2; 0,8. ¿Cuál es la suma de la diagonal?
a) 2,4 b) 3 c) 4,2 d) 3,4
Resolución:
Ordenamos en forma creciente.
0,2; 0,4; 0,6; 0,8; 1; 1,2; 1,4; 1,6; 1,6.
- Observamos que son nueve números que forman una sucesión creciente que al distribuirlos en un cuadrado mágico, la suma de las filas, columnas y diagonales deben ser iguales.
- Para ello, dibujamos un cuadro de 3 x 3 = 9 casilleros y agregamos casilleros auxiliares (en azul) al centro de cada lado del cuadrado.
- Como el lado del cuadrado tiene número impar de casilleros (3), distribuimos los números, en orden creciente, como se indica en el primer cuadrado.
- El número que queda en cada casillero auxiliar se introduce en el casillero vacío del lado opuesto.
Comprobamos que la suma de cualquier columna, fila o diagonal siempre es igual.
La suma de la diagonal: 0,8 + 1 + 1,2 = 3
La respuesta es b.
6) ¿Qué número sigue en:
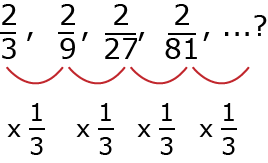
$\frac{1}{8}$, $\frac{2}{9}$, $\frac{2}{27}$, $\frac{2}{81}$,...?
a) $\frac{2}{162}$ b) $\frac{2}{729}$ c) $\frac{2}{108}$ d) $\frac{2}{243}$
Resolución:
Buscamos la ley de formación y observamos que es multiplicar $\frac{1}{3}$ al número anterior,
Aplicamos la ley de formación y hallamos "?"
$\frac{1}{8}$ $\bullet \; \frac{1}{3}$ = $\frac{2}{9}$
$\frac{2}{9}$ $\bullet \; \frac{1}{3}$ = $\frac{2}{27}$
$\frac{2}{27}$ $\bullet \; \frac{1}{3}$ = $\frac{2}{81}$
$\frac{2}{81}$ $\bullet \; \frac{1}{3}$ = $\frac{2}{243}$
? = $\frac{2}{243}$
La respuesta es d.
7) En $\frac{19}{2}$; $\frac{15}{2}$; 5,5; 3,5; x. El valor de "x" es:
a) $\frac{3}{2}$ b) $\frac{7}{5}$ c) $\frac{7}{2}$ d) $\frac{11}{2}$
Resolución:
Convertimos las fracciones a decimales:
$\frac{19}{2}$ = 9,5 $\frac{15}{2}$ = 7,5
Remplazamos:
9,5; 7,5; 5,5; 3,5; x
Buscamos la ley de formación y observamos que es restar 2 al número anterior,
Aplicamos la ley de formación y hallamos "x"
9,5 - 2 = 7,5
7,5 - 2 = 5,5
5,5 - 2 = 3,5
3,5 - 2 = x
x = 1,5 = $\frac{3}{2}$
La respuesta es a.
8) En $\frac{1}{2}$, $\frac{2}{6}$, $\frac{4}{18}$, $\frac{8}{54}$, $\frac{A}{B}$. El valor de A + B es:
a) 146 b) 178 c) 164 d) 187
Resolución:
Buscamos la ley de formación y observamos que es multiplicar $\frac{2}{3}$ al número anterior,
Aplicamos la ley de formación y hallamos "A + B"
$\frac{1}{2}$ $\bullet \; \frac{2}{3}$ = $\frac{2}{6}$
$\frac{2}{6}$ $\bullet \; \frac{2}{3}$ = $\frac{4}{18}$
$\frac{4}{18}$ $\bullet \; \frac{2}{3}$ = $\frac{8}{54}$
$\frac{8}{54}$ $\bullet \; \frac{2}{3}$ = $\frac{16}{162}$
$\frac{16}{162}$ = $\frac{A}{B}$
A + B = 16 + 162 = 178
La respuesta es b.
9) ¿Qué número sigue en
$\frac{2}{7}$, $\frac{5}{7}$, $\frac{8}{7}$, $\frac{11}{7}$, ...?
a) 4 b) 3 c) 2 d) 1
Resolución:
Buscamos la ley de formación y observamos que es sumar $\frac{3}{7}$ al número anterior.
Aplicamos la ley de formación y hallamos "?"
$\frac{2}{7}$ + $\frac{2}{3}$ = $\frac{5}{7}$
$\frac{5}{7}$ + $\frac{2}{3}$ = $\frac{8}{7}$
$\frac{8}{7}$ + $\frac{2}{3}$ = $\frac{11}{7}$
$\frac{11}{7}$ + $\frac{2}{3}$ = $\frac{14}{7}$
? = $\frac{14}{7}$ = 2
La respuesta es c.
10) ¿Cuál es el valor de "x"?
$\frac{1}{5}$ $\left ( \frac{1}{2} \right )$ $\frac{2}{5}$
$\frac{3}{2}$ (3) $\frac{1}{2}$
$\frac{1}{2}$ (x) $\frac{4}{3}$
a) $\frac{3}{8}$ b) $\frac{4}{6}$ c) $\frac{5}{6}$ d) $\frac{3}{7}$
Resolución:
Para obtener el término del medio, buscamos la relación entre términos extremos. observamos en la 1ª y 2ª fila se trata de una división.
Aplicamos la ley de formación en la 3ª fila para hallar el valor de "x"
$\frac{1}{5}$ $\div $ $\frac{2}{5}$ = $\frac{1}{2}$
$\frac{3}{2}$ $\div $ $\frac{1}{2}$ = 3
$\frac{1}{2}$ $\div $ $\frac{4}{3}$ = $\frac{3}{8}$
x = $\frac{3}{8}$
La respuesta es a.
11) ¿Cuál es el número que le falta?
a) $\frac{3}{8}$ b) $\frac{9}{64}$ c) $\frac{6}{16}$ d) $\frac{9}{6}$
Resolución:
Buscamos una relación entre los números que están colocados unos frente al otro como: $\frac{1}{3}$ y $\frac{1}{9}$, el número mayor se multiplica por si mismo, se obtiene el número opuesto.
$\frac{1}{3}$ $\bullet \; \frac{1}{3}$ = $\frac{1}{9}$
$\frac{2}{7}$ $\bullet \; \frac{2}{7}$ = $\frac{4}{49}$
$\frac{3}{8}$ $\bullet \; \frac{3}{8}$ = $\frac{9}{64}$
? = $\frac{9}{64}$
La respuesta es b.
12) ¿Cuál es el valor de "x"?
a) $\frac{18}{6}$ b) $\frac{19}{6}$ c) $\frac{20}{6}$ d) $\frac{21}{6}$
Resolución:
Buscamos una relación entre los números iniciamos desde $\frac{1}{6}$ sumamos $\frac{4}{6}$ en forma horaria y se obtienen el número siguiente.
$\frac{1}{6}$ + $\frac{4}{6}$ = $\frac{5}{6}$
$\frac{5}{6}$ + $\frac{4}{6}$ = $\frac{9}{6}$
$\frac{9}{6}$ + $\frac{4}{6}$ = $\frac{13}{6}$
$\frac{13}{6}$ + $\frac{4}{6}$ = $\frac{17}{6}$
$\frac{17}{6}$ + $\frac{4}{6}$ = $\frac{21}{6}$
x = $\frac{21}{6}$
La respuesta es d.
13) Hallar el valor de "x".
0,5 (5) 0,1
1,6 (8) 0,2
7,5 (x) 0,5
a) 5 b) 10 c) 15 d) 20
Resolución:
Para obtener el término del medio, buscamos la relación entre términos extremos. observamos en la 1ª y 2ª fila se trata de una división.
Aplicamos la ley de formación en la 3ª fila para hallar el valor de "x"
0,5 $ \div $ 0,1 = 5
1,6 $\div $ 0,2 = 8
7,5 $\div $ 0,5 = 15
x = 15
La respuesta es c.
14) Hallar el valor de "x".
$\frac{1}{3}$ $\frac{4}{9}$ $\frac{1}{3}$
$\frac{2}{5}$ $\frac{9}{25}$ $\frac{1}{5}$
$\frac{4}{7}$ x $\frac{1}{7}$
a) $\frac{16}{49}$ b) $\frac{25}{49}$ c) $\frac{10}{14}$ d) $\frac{5}{14}$
Resolución:
Para obtener el término del medio, buscamos la relación entre términos extremos. observamos en la 1ª y 2ª fila se trata de una suma y el resultado obtenido lo multiplicamos por dicho resultado que se obtuvo en la suma.
Aplicamos la ley de formación en la 3ª fila para hallar el valor de "x"
$\frac{1}{3}$ + $\frac{1}{3}$ = $\frac{2}{3}$ $\bullet \;\;\frac{2}{3}$ = $\frac{4}{9}$
$\frac{2}{5}$ + $\frac{1}{5}$ = $\frac{3}{5}$ $\bullet \;\;\frac{3}{5}$ = $\frac{9}{25}$
$\frac{4}{7}$ + $\frac{1}{7}$ = $\frac{5}{7}$ $\bullet \;\;\frac{5}{7}$ = $\frac{25}{49}$
x = $\frac{25}{49}$
La respuesta es b.









No hay comentarios.:
Publicar un comentario