ÁREA DE REGIONES SOMBREADAS

1) TRASLACIÓN DE ÁREAS SIMÉTRICAS.

Ejemplos.

Si ABCD es un cuadrado de lado "L", calcular el área de la región sombreada.

Resolución.

Trazamos diagonales del cuadrado y transponemos las áreas de las regiones sombreadas.

De la figura, el área de la región sombreada es la mitad del área total = $\frac{L^{2}}{2}$

SI ABCD es un cuadrado de lado "m", calcular el área de la región sombreada.

Resolución.

Se trazan rectas paralelas a los lados y trasladamos las regiones sombreadas:

Luego, El área de la región sombreada es la mitad del área total.

$A_{somb}=\frac{m^{2}}{2}$

Hallar el área de la región sombreada, si el lado del cuadrado mide 4 m.

 Resolución.

Se trazan diagonales y transponiendo áreas sombreadas.

El área sombreada es la mitad del área del cuadrado; entonces:

$A_{somb}=\frac{4^{2}}{2}=8$

2) DIFERENCIA DE ÁREAS

Ejemplos.

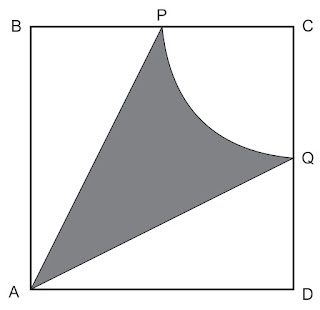
Si ABCD es un cuadrado de 8 cm de lado, además P y Q son puntos medios. Calcular el área de la región sombreada.

Resolución.

Del gráfico:

La figura "S" representa la cuarta parte de un circulo las dos figuras "a" juntas representan la mitad del cuadrado.

Luego, el área sombreada será:

$A_{somb}=area\; \;  \square ABCD-\left [ \frac{area\; \square ABCD}{2}+\frac{area\;  del\; \bigcirc CPD}{4} \right ]$

$A_{somb}=64\; cm^{2}-\left [ \frac{64\; cm^{2}}{2}+\frac{\pi (4\; cm)^{2}}{4} \right ]$

$A_{somb}=64\; cm^{2}-\left [ 32\; cm^{2}-4\pi cm^{2} \right ]$

$A_{somb}=64\; cm^{2}-32\; cm^{2}-4\pi cm^{2}$

$A_{somb}=32\; cm^{2}-4\pi cm^{2}$

$A_{somb}=4(8-\pi)cm^{2}$

Si "O" es centro del cuadrado ABCD de 12 cm de lado, entonces el área de la región sombreada será:

Resolución.

Las dos figuras "S" representan la mitad de un círculo, y la figura "C" representa la cuarta partes del cuadrado. 

Luego:

$A_{somb}=area\; \;  \square ABCD-\left [ 2S-C \right ]$

$A_{somb}=144\; cm^{2}-\left [ \frac{\pi (6)^{2}cm^{2}}{2} -\frac{144\; cm^{2}}{4}\right ]$

$A_{somb}=144\; cm^{2}-\left [ \pi 18\; cm^{2}-36\; cm^{2} \right ]$

$A_{somb}=144\; cm^{2}-\pi 18\; cm^{2}+36\; cm^{2}$

$180\;cm^{2}-18\pi\; cm^{2}$

Hallar el área de la región sombreada.

Resolución.

En el cuadrado la figura "S" es la cuarta parte de un círculo, entonces

$A_{somb}=area\; cuadrado\; \square ABCD-4S$

$A_{somb}=16\; m^{2}-4\frac{\pi R^{2}}{4}$

$A_{somb}=16\; m^{2}-4\frac{\pi. 2^{2}\; m^{2}}{4}$

$A_{somb}=16\; m^{2}-4\pi \;  m^{2}$

$A_{somb}=4(4\; m^{2}-\pi \; m^{2})$

Hallar el área sombreada.

Resolución.

la figura "S" es una cuarta partes de un círculo y "a" es el triángulo.

$A_{somb}=area\; cuadrado\; \square ABCD-\left [ 2S+2a \right ]$

$A_{somb}=16\; m^{2}-\left [ 2\frac{\pi R^{2}}{4}+2(2\; m^{2}) \right ]$

$A_{somb}=16\; m^{2}-\left [ 2\frac{\pi. 2^{2}\; m^{2}}{4}+2(2\; m^{2}) \right ]$

$A_{somb}=16\; m^{2}-\left [ 2\pi \; m^{2}-4\; m^{2} \right ]$

$A_{somb}=16\; m^{2}-2\pi \; m^{2}-4\; m^{2}$

$A_{somb}=12\; m^{2}-2\pi \; m^{2}$

$A_{somb}=2(6\; m^{2}-\pi \; m^{2})$

3) ÁREAS POR MEDIANAS

Ejemplos.

Si ABCD es un cuadrado de lado "a" y además "M" es un punto medio. calcular el área de la región sombreada.

Resolución.

Del gráfico.

Por la propiedad de las medianas, el área sombreada es:

$A_{somb}=\frac{a^{2}}{12}$

Si ABCD es un cuadrado de lado "a" y además "N" es punto medio. Calcular el área de la región sombreada.

Resolución.

Del gráfico.

Por propiedad de las medianas:

$A_{somb}=\frac{a^{2}}{3}$

4) ÁREA POR TANGENTES

Ejemplos.

Si ABCD es un cuadrado de 16 cm de lado; además M, N y P son puntos de tangencia, calcular el área de la región sombreada.

Resolución.

Aplicando Pitágoras.

$(2+R^{2})=2^{2}+(8-R)^{2}$

$4+4R+R^{2}=4+64-19R+R^{2}$

$4R+16R=64$

$20R=64$

$R=\frac{64}{20}$

$R=\frac{16}{5}\; cm^{2}$

$A_{somb}=\pi R^{2}$

$A_{somb}=\pi \left ( \frac{16}{5}\; cm^{2} \right )$

$A_{somb}=\pi \frac{256}{25}\; cm^{2}$

Calcular el área de la región sombreada de la siguiente figura: Si ABCD es un cuadrado de lado "a".

Resolución.

Por traslación de áreas

Luego.

el área sombreada será:

$A_{somb}=\frac{\pi R^{2}}{2}$

$A_{somb}=\frac{\pi \left ( \frac{a}{2} \right )^{2}}{2}$

$A_{somb}=\frac{\pi a^{2}}{8}$

Calcular el área de la región sombreada, si el lado del cuadrado es "L".

Resolución.

El área de la región sombreada es:

$A_{somb}=\frac{L.L}{2}$

$A_{somb}=\frac{L^{2}}{2}$