1) REGLA DEL TANTO POR CIENTO
Nos indica una relación entre una parte y la unidad que ha sido dividida en 100 partes iguales. Es decir:
Luego.
Entonces
Observaciones:
a) PORCENTAJE A FRACCIÓN:
b) FRACCIÓN A PORCENTAJE
Importante:
Ejemplos.
¿Qué porcentaje es 3 de 5?
¿Qué porcentaje es 3 de 4?
c) PORCENTAJE DE UNA CANTIDAD
Calcular el 30% de 90:
Calcular el 20% de 40:
Calcular el 20% del 60% del 50% de 40:
En general.
d) PORCENTAJE DE PORCENTAJE
Calcular el 30% de 70%:
Calcular el 20% de 80% del 50%:
En general.
e) TANTO POR CIENTO MÁS.
Calcular el 20% más de 40 <> Calcular el 120% de 40=48. Es decir:
Calcular el 40% más 20 <> Calcular el 140% de 20=28. Es decir:
En general.
Calcular al a% más de N <> Calcular (100+a)% de N
f) TANTO POR CIENTO MENOS.
Calcular el 30% menos de 30 <> Calcular el 70% de 30=21. Es decir:
Calcular el 40% menos de 80 <> Calcular el 60% de 80=48. Es decir:
En general.
Calcular al a% menos de N <> Calcular el (100-a)% de N
g) OPERACIONES CON PORCENTAJES.
30%A + 40%A = 70%A
70%B - 20%B =50%B
N - 40%N = 60%N
2P + 10%P = 200%P + 10%P = 210%P
20% más = 120%
5% menos = 95%
Relación parte todo.
Ejemplos.
¿Qué tanto por ciento es 15 de 40?
¿Qué porcentaje de 75 es 25 ?
¿Qué porcentaje de "A" es "B"?
En una reunión de 60 personas en 20% son hombres y el resto mujeres. ¿Qué porcentaje de las mujeres son los hombres?
Resolución.
Total de personas: 60
Entonces, el número de mujeres:
60 - 12 = 48 = M
Luego, qué porcentaje de M es H; aplicando la formula se tiene:
Es decir:
En una reunión se sabe que el 30% del número de hombres es igual al 40% del número de mujeres . ¿Qué porcentaje del total son hombres?
Resolución.
Son : H hombres y M mujeres
Del dato
De donde:
Total de personas: 7k
Luego los hombres del total representan:
2) DESCUENTOS SUCESIVOS
a) PARA DOS DESCUENTOS SUCESIVOS.
Sean a% y b% dos descuentos sucesivos, entonces el descuento único o efectivo se determina por:
Ejemplo.
¿A qué descuento único equivalen dos descuentos sucesivos del 20% y 40% de una cantidad?
Resolución.
b) PARA "n" DESCUENTOS SUCESIVOS.
En este caso se aplica el tanto por ciento menos para determinar lo que se debe pagar, en consecuencia, el descuento único se obtiene restando del 100%.
En general, para "n" descuentos sucesivos.
Ejemplo.
Tres descuentos sucesivos del 10%, 30% y 50% equivalen a un único descuento de:
Resolución.
3) AUMENTOS SUCESIVOS
a) PARA DOS AUMENTOS SUCESIVOS
Sean a% y b% dos aumentos sucesivos, entonces el descuento único o equivalente se determina por:
Ejemplo.
Dos incrementos sucesivos del 20% y 30%. ¿A qué aumento equivale?
Resolución.
b) PARA "n" AUMENTOS SUCESIVOS.
En este caso se aplica el tanto por ciento más para determinar lo que recibe al final; en consecuencia, el aumento único se obtiene restándole 100%.
En general, para "n" aumentos sucesivos.
Ejemplo.
Tres aumentos sucesivos del 10%, 60% y 80% equivalen a un único aumento de:
Resolución
Aplicando la fórmula.
APLICACIONES COMERCIALES
Ejemplo.
Juan compra una maquina a $400,00 (precio de costo) y decide ofrecerla a $500,00 (precio fijado), sin embargo al momento de la venta lo hace por $420,00 (precio de venta). se realiza un descuento del (500,00 - 420,00 =$80,00)(ganancia bruta), pero esta operación comercial genera gastos de $5,00, o sea gano realmente: 20,00 - 5,00 = $15,00 (ganancia neta). Veamos:
Luego del gráfico.
De donde:
Ejemplo.
Para fijar el precio de venta de un artículo se aumento su costo de 80%. Pero al vendedor se hizo una rebaja del 40%. ¿Qué tanto por ciento del costo se ha ganado?
Resolución.
Sea "x" el precio de costo del artículo, entonces:
Ahora:
Luego:
Un comerciante compra una mercadería y la vende con un beneficio del 8% sobre el precio de la compra. Si ganara el 8% sobre el precio de venta resultaría una ganancia de $8,00 más. Hallar el precio de compra.
Resolución.
Luego.
De donde:







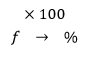
















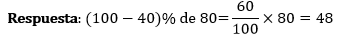









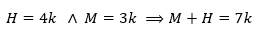







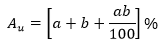










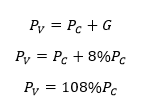
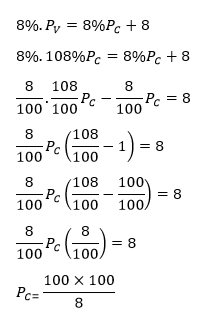

No hay comentarios.:
Publicar un comentario