1) DEFINICIÓN
Son los números de la forma:
Donde:
a : Es el denominador e indica las partes en las que se ha dividido la unidad.
b : Es el numerador que representa las partes que se ha tomado de la unidad.
Ejemplos explicativos.
Un abuelo dejó su herencia entre sus 7 nietos. Si todos recibieron por igual, para saber que parte recibirán 3 de ellos primero dividiremos la herencia en 7 partes iguales, de las cuales consideremos sólo 3 partes.
A los tres hermanos le corresponde
Luego.
¿Qué parte de 7 es 3?
¿Qué parte de 7 representa 5?
¿Qué parte es 13 respecto de 18?
Finalmente.
En general
Observaciones.
2) OPERACIONES CON FRACCIONES
3) CLASIFICACIÓN DE LAS FRACCIONES
Sea la fracción:
Donde:
a) FRACCIÓN PROPIA. (N<D)
Cuando el numerador es menor que el denominador, es decir, que la fracción es menor que la unidad.
Ejemplo.
b) FRACCIÓN IMPROPIA. (N>D)
Cuando el numerador es mayor que el denominador, es decir, que la fracción es mayor que la unidad.
Ejemplo.
Nota:
Toda fracción impropia se puede expresar por un número llamado fracción mixta.
c) FRACCIÓN REDUCTIBLES
(N y D tienen divisores comunes diferentes de la unidad).
Cuando el denominador no son primos entre si.
Ejemplo.
d) FRACCIÓN IRREDUCIBLE. (N y D son PESI)
Cuando el denominador y denominador son primos entre si.
Ejemplo.
Nota:
De ellos se desprenden las fracciones equivalentes.
e) FRACCIONES HOMOGÉNEAS.
Dos o más fracciones son homogéneas si tienen igual denominador.
Ejemplo.
Nota:
En fracciones homogéneas es mayor la que tiene el mayor numerador.
f) FRACCIONES HETEROGÉNEAS.
Dos o más fracciones son heterogéneas si uno de los denominadores es diferente a los demás.
Ejemplo.
4) VARIACIÓN DEL VALOR DE UNA FRACCIÓN.
a) SIGNOS DE UNA FRACCIÓN.
En una fracción debe distinguirse tres signos:
- Signo que antecede a la fracción.
- Signo del numerador.
- Signo del denominador.
Ejemplo.
b) CAMBIOS DE SIGNO DE UNA FRACCIÓN.
Si de los tres signos de una fracción se cambian dos de ellos, la fracción no varia.
Ejemplo.
Ejercicio.
Calcular el valor de:
Resolución.
c) FRACCIÓN DE UN NÚMERO DADO.
(de, del, de los <> a multiplicar)
Calcular:
Ejemplos.
d) MÉTODO DE LA REDUCCIÓN A LA UNIDAD.
Este método se aplica en aquellos problemas que relacionan:
Obra, trabajo, caños, grifos, piscinas, desagües, etc., donde no se conoce la magnitud del trabajo o tarea pero si es conocido el tiempo total que se necesita para hacer dicha obra.
El procedimiento consiste en determinar el avance por unidad del tiempo, para lo cual basta tomar la inversa al tiempo total.


















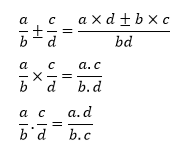










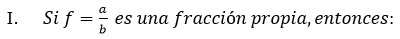







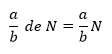
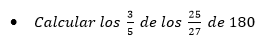
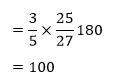
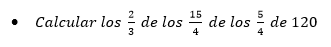
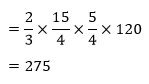
No hay comentarios.:
Publicar un comentario