PLANTEO DE ECUACIONES
1) OBJETIVO ESPECÍFICO
a) Traducir del lenguaje común al lenguaje simbólico.
b) Resolver problemas que originan ecuaciones de una sola incógnita (lineales) o con dos o más incógnitas.
c) Plantear y resolver problemas de ecuaciones cuadráticas (segundo grado).
d) Resolver una ecuación diofántica por cualquiera de los métodos.
2) CONCLUSIÓN
Todo problema es una proposición, donde se nos pide calcular cantidades que también son conocidas como INCÓGNITAS empleando las relaciones que se nos dan entre las incógnitas y los datos.
La relación entre INCÓGNITAS y DATOS nos permite formar la ecuación. Para la resolución de los problemas hay que seguir los siguientes pasos:
- Lectura detallada del enunciado.
- Identificación de incógnitas y datos.
- Relación entre la incógnita y datos, llamada también planteo de ecuación.
- Verificación de resultados obtenidos.
Observaciones.
Generalmente en el planteamiento de una ecuación se utilizaran las letras x, y, a, b, etc.
Ejemplos.
Traducir el lenguaje matemático (forma simbólica), cada uno de los siguientes enunciados:
- El triple de un número aumentado en su mitad.
- El cuadrado de un número aumentado en cinco.
- La suma de los cubos de dos números .
- El cubo de la suma de dos números.
- La suma de dos números consecutivos es 99. x + (x + 1)=99
- La suma de tres números pares consecutivos es 36.
2x + 2x + 2 + 2x + 4 = 36
- La suma de tres números pares impares consecutivos es 45.
2x + 1 + 2x + 3 + 2x + 5 = 45
- Gastó la tercera parte de lo que no gastó.
Sea "n" el total y gasto "x" entonces lo que no gastó es (n - x) y su tercera parte es
- El número de varones es la quinta parte del total de reunidos.
Sea "n" el total, su quinta parte es:
- "a" es 7 veces "b": a = 7b
- "a" e 7 veces más que "b": a = 7 + b
- "a" e 7 veces mayor que "b": a = 7b
- Dos números están en relación de 3 a 5.
- "M" excede a "N" en "x": M - x = N
- El exceso de "M" sobre "N" es "Z": M - Z = N
- "a" es excedido por "b" en 20: b - 20 = a
- Un número excede a 20 tanto como 110 excede a dicho número:
- La diferencia de dos números es 20: a - b = 20
- Un número es menor en 42 que el cuadrado de su consecutivo:
Ejemplos.
En un pueblo a cada habitante le corresponde 60 litros de agua por día. Hoy a aumentado la población en 40 habitantes y le corresponde a cada uno 3 litros menos. ¿Cuál es el número de habitantes?
Resolución.
Sea "n" el numero de habitantes.
En 1 día recibe: 60 x n de agua.
Luego "n" aumenta en 40: n + 40
Entonces, en 1 día reciben: (n + 40)(60 - 3)
Igualando se tiene: 60n = (n + 40) x 57
De donde: n = 760
Un comerciante empleó 2 750 dólares en comprar pantalones a 40 dólares y camisas a 25 dólares. si el número de pantalones y el número de camisas que se compró es 80, ¿Cuántos pantalones compró?
Resolución.
Sea "P" el número de pantalones.
Sea "C" el número de camisas.
Dato:
De (1):
Remplazando en (2):
Entre dos personas tienen "x" dólares, si una de ella diera "a" dólares a la otra las dos tendrían iguales cantidades. ¿Cuánto tiene la persona que posee más?
Resolución.
Sea:
P(1): número de dólares de la primera persona.
P(2): número de dólares de la segunda persona.
Dato.
P(1) + P(2) = x ............................................(1)
P(1) - a = P(2) + a => P(1) - P(2) = 2a......... (2)
Sumando (1) + (2)
La persona que posee más tiene:
Una mula y un caballo llevan sobre sus lomos pesados sacos. La mula le dice al caballo "si yo tomara dos sacos de los tuyos mi carga seria el doble que la tuya". El caballo le dice a la mula "Es cierto, pero si yo tomara dos sacos de los tuyos nuestras cargas se igualarían". ¿Cuántos sacos hay en total?
Resolución.
Sea:
C: número de sacos del caballo.
M: número de sacos de la mula.
M + C = n
De los datos.
M + 2 = 2(C - 2)...................(1)
C + 2 = M - 2.......................(2)
(1) + (2) => C = 10
Remplazando "C" en (2):
M = 14
En total hay 24 sacos.
EDADES
Por la variedad de problemas existentes lo dividiremos en dos grandes grupos:
1) CUANDO INTERVIENE LA EDAD DE UN SOLO SUJETO.
Es recomendable resolver el problema planteando una simple ecuación.
Ejemplos.
Dentro de 6 años Juan tendrá 3 veces la edad que tuvo hace 4 años.
Resolución.
Sea "x" la edad actual de Juan.
Luego.
La edad de Juan es 9 años.
Marcelo tenía en el año 1969 tantos años como el doble del número formado por las 2 últimas cifras del año de su nacimiento. ¿Cuántos años tendrá Marcelo el año 2009?
Para dar solución a este problema, previamente.
Año de nacimiento + Edad = Año actual
Año de nacimiento + Edad = Año actual - 1
Resolución.
AN = Año de nacimiento
Ex = Edad
AA = Año actual.
Luego.
AN + Ex = AA
19ab + 2ab = 1969
1900 + ab + 2ab = 1969 => 3ab = 69
De donde : ab = 23
Entonces:
Ex - AA = AN
Ex = 2009 - 1923 => Ex = 86 años
Marcelo tendrá en el año 2009 => 86 años.
2) CUANDO INTERVIENE LA EDAD DE DOS O MÁS SUJETOS.
Se presenta dos casos:
a) Tiempos específicos.
Cuando se especifican cuantos años antes o después (hace 3 años, haces 5 años, dentro de 12 años, etc.) se recomienda resolver el problema "planteando ecuaciones" tal como se vera a continuación.
Ejemplo.
Miguel tiene el triple de los años que tiene Lucia; hace 6 años la suma de sus edades era de 40 años, ¿Qué edad tendrá Lucia dentro de 17 años?
Resolución.
Como se observa en el problema, la presencia de dos sujetos (Miguel y Lucia), pero además especifican el tiempo (hace 6 años).
Luego:
Hace 6 años
Miguel: 3x 3x - 6
Lucia: x x - 6
Además:
3x - 6 + x - 6 = 40 => x = 13
Dentro de 17 años Lucia tendrá 30 años.
b) Tiempos no especificados
Cuando no especifican cuantos años antes o después, en un problema en el cual intervienen dos, tres o más sujetos. se recomienda el uso de una tabla de doble entrada.
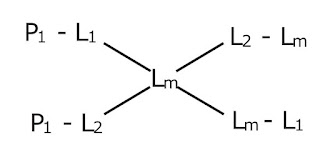
Observaciones.
La suma de "aspas" es igual.
12+29=20+21
21-35=29+27
12+35=20+27
La diferencia de edades es cte.
cte = 29 - 21 = 20 - 12 = 35 - 27
Ejemplo.
Daniel le dijo a Fabiola, yo tengo 5 veces la edad que tú tenías cuando yo tenía la edad que tienes y cuando tengas la edad que tengo, la suma de nuestras edades será 60 años. ¿Cuántos años tiene Fabiola?
Resolución.
2y=2x
y=3x
10x = 60 - 5x + y
15x -y = 60
15x - 3x = 60
12x = 60 => x=5
Luego.
y = 15
La edad de Fabiola es igual a 15 años.
MÓVILES
En este tema trata del estudio del movimiento de los cuerpos y de sus características como son el espacio, tiempo y velocidad.
1) ECUACIÓN FUNDAMENTAL.
Dado un cuerpo que se mueve desde un punto "A" hasta "B", como indica en la figura.
Se cumple.
Despejando.
Donde:
e = Espacio
t = Tiempo
v = Velocidad
Observación.
Es importante verificar que todas las variables tengan unidades compatibles.
2) TIEMPO DE ENCUENTRO (Te)
Es el tiempo en que demora en encontrarse dos móviles viajando en sentidos contrarios. Así, dados dos móviles que se mueven en sentidos contrarios como la siguiente figura.
Para calcular después de cuánto tiempo se encontraran, se aplica la siguiente fórmula.
Donde.
Ejemplo.
Dos tres parten a encontrarse desde poblaciones separadas a 870 Km, al mismo tiempo el tren de pasajeros viaja a 80 Km/h y el tren de carga a 65 Km/h. ¿Cuántas horas necesitaran para encontrarse?
Resolución.
3) TIEMPO DE ALCANCE (Ta)
Se refiere al tiempo que demora un móvil en alcanzar a otro que se mueve en el mismo sentido, como la siguiente figura.
Observación:
Para calcular después de qué tiempo uno alcanza al otro, se aplica la siguiente fórmula.
Donde:
Ejemplo.
Cristóbal salió en su auto con una velocidad inicial de 40 Km/h; dos horas después Andrea salió del mismo lugar, ella manejó por la misma carretera a 50 Km/h. ¿Cuántas horas habrá manejado Andrea cuando alcanzo a Cristóbal?
Resolución.
4) CRITERIO DE CORRIENTES
Para criterio de corrientes sólo hay que considerar que cuando se navega a favor de la corriente las velocidades del barco y la corriente se suman y cuando se navega contra de la corriente las velocidades se restan.
Ejemplo.
Cuando un bote navega a favor de la corriente demora 2 horas en recorrer 12 Km. Pero cuando navega en contra demora 4 horas más en recorrer los 12 Km. ¿Cuál es la velocidad del bote?
Resolución.
Caso (1). Navegando a favor de la corriente
Donde:
Caso (2). Navegando en contra de la corriente.
Donde.
Luego igualamos (1) y (2) se tiene
Reemplazando en (1) tenemos.
Entonces.
Finalmente, la velocidad del bote es: 4 Km/h
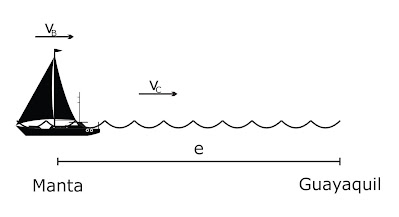
La rapidez de un bote que va de ida es 20 Km/h; cuando va de regreso contra la corriente logra una rapidez de 15 Km/h. Hallar el espacio recorrido si va de Manta a Guayaquil, sabiendo además que de ida demora 5 horas menos que de regreso.
Resolución.
De regreso.
Igualando (1) = (2)
5) VELOCIDAD PROMEDIO
Cuando un móvil cambia de velocidad con el tiempo se desea conocer una velocidad que remplace a todas las anteriores y que desarrolle el mismo espacio
en el mismo tiempo. Esta velocidad es llamada VELOCIDAD PROMEDIO
Así tenemos.
Luego, la velocidad promedio se calcula con la siguiente fórmula.
Donde:
6) CRITERIOS DE TRENES
Para cualquier problema de trenes se utiliza como fórmula básica la ecuación fundamental del movimiento.
Aplicación
a) Un tren viaja a 20 Km/s, y se demora 4 segundos en pasar delante de un observador. ¿Cuál es la longitud del Tren?
Resolución.
Graficando
Donde:
L = Longitud del tren
Aplicando la ecuación fundamental
e = v . t
L = 20 . 4
L = 80 m
b) Un tren demora 8 segundos en pasar delante de un observador y 10 segundos en pasar totalmente por un túnel de 400 metros de longitud. ¿Cuál es la longitud del tren?
Resolución.
- Pasa delante de la persona
- Pasa por el túnel.
De donde:
MEZCLA Y ALEACIÓN
1) MEZCLA
Se llama mezcla a la unión de varias sustancias, conservando cada una de ellas su propia naturaleza.
Desde el punto de vista comercial, la mezcla se realiza con el objeto de establecer el precio promedio, de manera que no se produzca pérdida ni ganancia.
2) CLASE DE MEZCLA
a) REGLA DE MEZCLA DIRECTA
Su objetivo es el de calcular el precio promedio o medio, conociendo la cantidad de los ingredientes que intervienen y sus respectivos precios unitarios.
Ejemplo.
Santiago mezcla 40 litros d alcohol de 6 dólares el litro con 60 litros de alcohol de 11 dólares el litro. ¿Cuál será el precio promedio de la mezcla)
Resolución.
b) REGLA DE LA MEZCLA INVERSA
Tiene como objeto calcular las proporciones en que intervienen los ingredientes, conocidos sus precios unitarios y el precio medio de las mezclas.
Datos:
Donde:
Incógnitas: Cantidad de los ingredientes (x, y)
Resolución
- Al vender "x" unidades del primero se pierde:
- Al vender "y" unidades del segundo se gana:
- Pero como en la mezcla no se gana ni se pierde:
Por lo tanto:
Como regla práctica.
Rodrigo tiene 100 litros de una mezcla que contiene vino de 4 dólares y 8 dólares el litro; si el precio medio de la mezcla es de 6,60 dólares. ¿Cuántos litros de vino más barato hay en la mezcla?
Resolución.
Luego:
La cantidad del vino más barato es 35 litros de 4 dólares.
c) MEZCLAS ALCOHÓLICAS
Grado de una mezcla alcohólica (G).
Es la relación que existe entre el volumen de alcohol puro (A) y el volumen total de la mezcla (V).
Nota.
El grado de una mezcla alcohólica se expresa en porcentaje, es decir en tanto por ciento.
Mezcla alcohólica directa.
Incógnita: Grado de la mezcla resultante
Ejemplo.
Se mezclan 40 litros de alcohol al 60% con 80 litros de alcohol al 30%. ¿Qué concentración tendrá la mezcla final?
Resolución.
3) ALEACIÓN
¿Qué es una ley de una aleación?
Es una aleación, la ley es una relación que existe entre el peso de metal fino y el peso total de la aleación. La liga de la aleación es la relación que existe entre el peso de metal ordinario y el peso total de la aleación.
La ley de las aleaciones en las cuales intervienen al oro generalmente se expresa en "kilates", de tal manera que.
- PROBLEMA DIRECTO
Incógnita
- PROBLEMA INVERSO
¿Qué es una amalgama?
Es aquella aleación en la cual interviene el mercurio.
Nota importante.
El oro puro tiene 24 kilates de ley.
La plata pura tiene 1000 mm de ley.
Ejemplo.
Se tiene dos barra de oro, en la primera el 80% del peso total es oro, en la segunda, cuyo peso es el doble de la anterior el 75% del peso total es oro. Si se mezclan ambas barras. ¿De cuántos kilates resultaría la aleación?
Resolución.
Luego:

















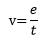



















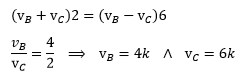















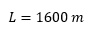



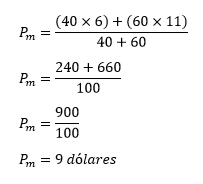


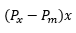



























No hay comentarios.:
Publicar un comentario