Es aquella que genera cuando definimos una aplicación u operación con respecto a un determinado conjunto.
1) LEY DE COMPOSICIÓN INTERNA
Dado un conjunto A={a, b, c, d,....} y la operación simbolizada por "*", se dice que la operación (*) es una ley de composición interna en A si se cumple las siguientes condiciones:
Si definimos en el conjunto de números naturales (N) tenemos:
Por lo tanto, se dice que la adición es una composición interna en los naturales.
Observación 1.
Usando un lenguaje conjuntista tenemos que:
Observación 2.
A una ley de composición interna se le llama "operación binaria", lo cual puede tener una presentación tabular (pitagórica).
Operación Binaria:
2) PROPIEDADES EVENTUALES DE UNA LEY DE COMPOSICIÓN
a) CLAUSURA.
b) CONMUTATIVA
c) ASOCIATIVA
d) EXISTENCIA DE UN ÚNICO ELEMENTO NEUTRO (e)
Observación.
a. La adición de los reales.
b. La multiplicación de los reales.
e) ELEMENTO SIMÉTRICO (a')
Observación.
a. La adición de los reales:
a' = -a = Elemento opuesto
f) OTRAS PROPIEDADES.
1) DISTRIBUTIVA
Se define para dos operaciones y un conjunto de elementos.
a*(b#c)=(a*b)#(a*c)
(b#c)*a=(b*a)#(c*a)
Se dice que la operación (*) es distributiva con respecto a la operación (#).
2) ELEMENTO REGULAR
Se define para la operación y un conjunto.
Si:
a*b=a*c => b=c
a= Elemento regular
Si todos los elementos de un conjunto son regulares en cierta operación, entonces la operación cumple la propiedad de SIMPLIFICACIÓN.
3) ELEMENTOS PERMUTABLES
Se define para una operación no conmutativa y para algún elemento de un conjunto dado.
4) IDEMPOTENCIA
Se define para la operación y un conjunto.
Ejemplos.
Se define la operación matemática siguiente.
Hallar:
[(3#2)#(1#0)]#(3#1)
Resolución.
De la tabla se obtiene:
3#2=2; 1#0=2; 3#1=3
Remplazando.
Se define en A ={1; 2; 3; 4}, la operación matemática mediante la siguiente tabla.
Hallar el valor de "a" en:
Resolución.
De la tabla.
Remplazando.
Se define en N la operación * mediante la siguiente tabla.
Calcule: 94 * 95
Resolución.
Se observa que la variación es linealmente tanto en forma horizontal (de 2 en 2 en cada fila), como verticalmente (de 6 en 6 en cada columna).
Luego se cumple: a * b = ma + nb + p
De la tabla.
1 * 1 = m(1) + n(1) + p = 3
m + n + p = 3 ...................(1)
1 * 2 = m(1) + n(2) + p = 5
m + 2n + p = 5 ...................(2)
2 * 1 = m(2) + n(1) + p = 9
2m + n + p = 9 ...................(3)
De donde: (2) - (1) => n=2, (3) - (1) => m=6
Remplazando en (1)
(m y n) se obtiene: p = -5
Entonces:
a * b = 6a + 2b - 5
94 * 95 = 6(94) + 2(95) - 5 = 749




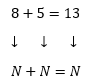























No hay comentarios.:
Publicar un comentario