Son un conjunto de proposiciones deducidas a partir de los axiomas del conjunto de los números reales, que trata sobre el estudio de los exponentes y las relaciones que se dan entre ellos.
Las operaciones que permiten la presencia de exponentes son la potenciación y la radicación.
A) POTENCIACIÓN
Es aquella operación de la forma
Donde: "b" es la base y "n" el exponente.
Definiciones.
A.1) EXPONENTE NATURAL
Ejemplos.
Nota.
A.2) EXPONENTE NULO
Ejemplos.
A.3) EXPONENTE NEGATIVO
Ejemplos.
A.3) EXPONENTE FRACCIONARIO
Ejemplos.
TEOREMAS
1) PRODUCTO DE BASES IGUALES
Ejemplos.
2) COCIENTE DE BASES IGUALES
Ejemplos.
3) POTENCIA DE POTENCIA
Ejemplos.
4) MULTIPLICACIÓN DE BASES CON EXPONENTES IGUALES
Ejemplos.
5) DIVISIÓN DE BASES CON EXPONENTES IGUALES
Ejemplos.
Propiedad inversa
Ejemplo.
B) RADICACIÓN EN R
Es aquella operación que se genera por la presencia del exponente fraccionario, que consiste en hallar una cantidad llamada raíz, y que elevada al valor del índice nos reproduce el radicando.
ALGORITMO
Donde:
Ejemplos.
EXISTENCIA Y UNIDAD DE LA RAÍZ
Ejemplos.
EXPONENTE FRACCIONARIO
Ejemplos.
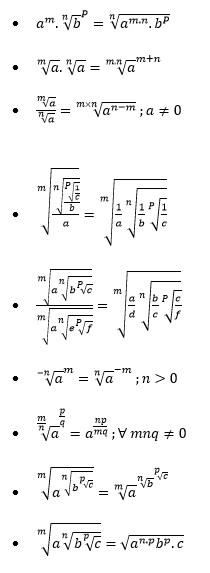
PROPIEDADES DE LA RADICACIÓN
Teorema:
Ejemplos.
Caso general.
PROPIEDADES AUXILIARES.
TEOREMAS ADICIONALES
2. Se presenta 2 casos:
a) si "k" es par.
b) si "k" es un número impar.
Observaciones.
En los teoremas (1) y (1), en el caso de que "n" sea un número par, el radicando "x" deberá ser no negativo.
TEOREMAS DE CONVERGENCIA
Ejemplo.
Con aplicación directa se tiene:
Ejemplo.
Con aplicación directa.
Ejemplo.
Por simetría S=x, entonces:
Ejemplo.
Entonces:
Hallar el valor de:
Demostración.
De la demostración: 0<3<e -----> Falso
Por lo tanto, el problema no cumple la condición:
ECUACIONES EXPONENCIALES ELEMENTALES
Una ecuación exponencial, es una igualdad literal, en la cual por lo menos uno de sus miembros contiene a la incógnita en el exponente. Esta ecuación será elemental si su conjunto solución se obtiene por la trasformaciones elementales.
Ejemplo.
Como 4, 8 y 16 son potencias de 2, se tiene:
Igualando exponentes se tendrá.
De donde:
OBTENCIÓN DE SOLUCIONES RACIONALES Y DE SOLUCIONES IRRACIONALES SIN APROXIMACIÓN.
Para la resolución de la ecuación elemental es preciso obtener las siguientes propiedades generales, a partir de transformaciones elementales por comparación explícita.
PROPIEDAD 1.
Ecuación de bases iguales.
PROPIEDAD 2.
(*) Ecuación explícita por reflexión.
(*) Exceptuando la relación numérica:
Que nos conducirá a la conclusión.
PROPIEDAD 3.
Ecuación de bases diferentes.
Donde A y B son primos entre si.
PROPIEDAD 4.
Ecuación explícita sin simetría.
Ejemplos.
Resolver la ecuación:
Determine el cociente de sus soluciones.
Resolución.
Luego.
Entonces.
Resolver.
Aplicando la suma de las cifras de:
Resolución.
Por simetría se tiene: x=-2006
Luego.
OBSERVACIONES.
Resolver


Igualdad numérica que coincide (4) del infinito continuo, el número 2 pertenece al intervalo de convergencia 0<2<e aproximadamente 2,71. Ahora si nos piden resolver la ecuación.
Diremos que es incompatible, debido a que la aproximación









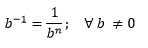


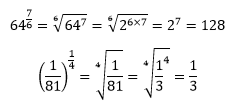

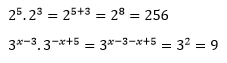









































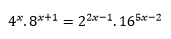

















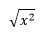



No hay comentarios.:
Publicar un comentario