Se denomina logaritmo del número "N" (N>0) en base "b" $(b>0\, \, \wedge \, \, b\neq 1)$ al exponente al cual se debe elevar la base "b" para obtener como resultado dicho número.
Siendo:
se define:
Donde:
- En el campo de los números reales no existen logaritmos de números negativos.
Ejemplo.
- La base de los logaritmos tienen que ser positiva y diferente de la unidad.
Ejemplo.
Estos logaritmos tienen base positiva y diferente de la unidad.
Ejemplos.
Hallar.
Resolución.
Sea "k" el logaritmo, entonces:
Hallar.
Resolución.
Hallar.
Resolución.
PROPIEDADES GENERALES DE LOS LOGARITMOS.
- Siendo
- Siendo
Además
- Si:
Si:
Además otras propiedades:
Ejemplo.
Calcular: 8a + 6b
Resolución.
Por definición.
PRINCIPALES SISTEMAS DE LOGARITMOS.
LOGARITMOS DECIMALES
Son aquellos cuya base es el número 10.
PROPIEDADES.
1. En este sistema de base 10 los logaritmos de los números mayores que uno son positivos y los logaritmos de los números menores que uno (pero mayores que cero) son negativos.
2. $log_{b}b^{n}=n$ (Siempre se cumple)
3. Característica y Mantisa.
Característica: Se llama así a la parte entera del logaritmo.
Mantisa: Es la parte decimal del logaritmo.
Ejemplo.
- Las características del logaritmo decimal de un número mayor que uno es igual al número de cifras que hay en su parte entera, menos uno.
Ejemplo.
- Las características del logaritmo decimal de un número menor que uno es negativa e igual al número de ceros que preceden a la primera cifra significativa (número diferente de cero), considerando incluso el cero de la parte entera si la hubiera.
Ejemplo.
SISTEMA DE LOGARITMOS NATURALES Y NEPERIANOS.
Llamados también hiperbólicos, son aquellos donde su base es el número "e" (inconmensurable o trascendente).
Se define:
e -----> Base de los logaritmos neperianos
También:
NOTACIÓN.
Se lee logaritmo neperiano o natural de N. Además:
LOGARITMO.
Se define como el logaritmo de la inversa de "N" en la misma base "b".
Siendo:
Entonces:
Ejemplos.
- ANTILOGARITMO.
Es otra forma de expresar la función exponencial. Se define:
A) PROPIEDADES
Ejemplos.
B) ECUACIONES LOGARÍTMICAS.
Conjunto de varias admisibles (C.V.A.) se obtiene de las condiciones (restricciones) que dan existencias a los logaritmos en R, en dicha ecuación.
Ejemplo.
C) CONJUNTO SOLUCIÓN DE UNA ECUACIÓN.
El conjunto solución (C.S.) se obtiene luego de una aplicación de las propiedades de los logaritmos en la ecuación. Dicho conjunto solución o selección necesariamente deben ser elementos del (C.V.A).
Ejemplo.
Resolver:
e indicar su solución o soluciones.
Resolución.
Luego.
Intersectando con el (C.V.A.). Se tiene:
Sólo satisface $x=\frac{1}{2}$; por lo tanto el conjunto solución es: $x=\frac{1}{2}$.




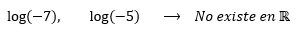



















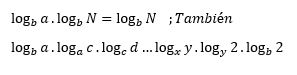


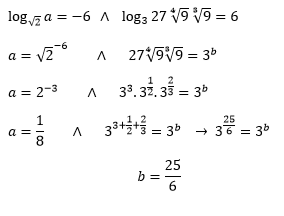















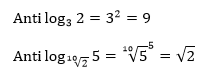

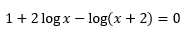
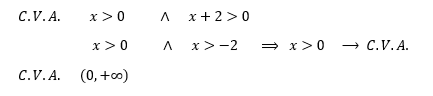
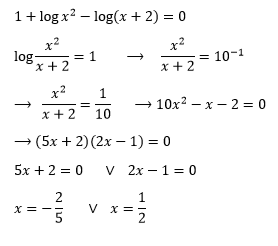

No hay comentarios.:
Publicar un comentario