Inecuaciones cuadráticas
Donde a, b y c son números reales, se llama inecuación cuadrática en x. si el símbolo < se remplaza por la

 , la inecuación
resultante también se denomina inecuación cuadrática.
, la inecuación
resultante también se denomina inecuación cuadrática.Puesto que puede escribirse, respectivamente, como
Propiedad de los signos de los productos
1. Si el producto de los números reales es positivo, los dos números tienen los mismos signos.
2. Si el producto de los números reales es negativo, entonces los dos números tienen signos opuestos.
Por
tanto, para resolver una inecuación  ,
debemos determinar cuando los dos factores son ambos positivos o ambos
negativos, porque entonces su producto será positivo. Una manera de ocuparse de
los signos de estos factores es haciendo un diagrama de signos, como sigue.
,
debemos determinar cuando los dos factores son ambos positivos o ambos
negativos, porque entonces su producto será positivo. Una manera de ocuparse de
los signos de estos factores es haciendo un diagrama de signos, como sigue.
Primero señalamos sobre una resta numérica los puntos por los cuales los factores son cero (en este caso – 3 y – 1). Como lo muestra la figura, estos puntos, llamados números críticos, dividen a la resta de intervalos. A continuación determinamos el signo de cada factor en cada uno de estos intervalos y utilizamos la propiedad (1) y (2). Ya que estos factores lineales no pueden cambiar de signo dentro de estos intervalos, basta con obtener el signo de cada factor solamente escogemos un valor de prueba de cada intervalo.
Por ejemplo.
En
el intervalo  ,
si utilizamos x = - 10 como valor de prueba, encontramos que tanto (x + 3) como
(x – 1) son negativos. Se deduce que su producto es positivo y se satisface la
ecuación.
,
si utilizamos x = - 10 como valor de prueba, encontramos que tanto (x + 3) como
(x – 1) son negativos. Se deduce que su producto es positivo y se satisface la
ecuación.
Para (– 3, 1), seleccionamos x = 0 como valor de prueba y encontramos que (x + 3) es positivo y (x – 1) es negativo. Así, el producto es negativo y la ecuación no se satisface.
Para
el tercer intervalo  ,
encontramos por un valor de prueba de x = 2 que tanto (x + 3) como (x – 1) son
positivos. En consecuencia, su producto es positivo.
,
encontramos por un valor de prueba de x = 2 que tanto (x + 3) como (x – 1) son
positivos. En consecuencia, su producto es positivo.
Finalmente,
debemos decidir si los números críticos son soluciones. Ya que (x + 3) (x – 1)
es igual a cero en los números críticos, la inecuación  ”mayor
que” no satisface. Por lo tanto, las soluciones las da la unión de los dos
intervalos
”mayor
que” no satisface. Por lo tanto, las soluciones las da la unión de los dos
intervalos  y
y  que
pueden escribirse como
que
pueden escribirse como  .
.
Ejemplos.
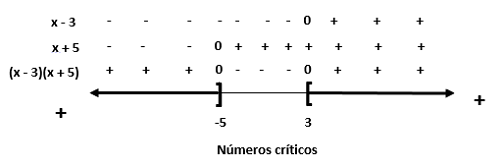
Ya que todos los términos diferentes de cero están a un lado de la inecuación comenzamos a factorizar:
A continuación desarrollamos un diagrama de signos.
Con
los números críticos 3 y –5. Puesto que la inecuación incluye un signo “mayor o
igual que”, los números críticos -5 y 3, que hacen el producto (x – 3) (x + 5)
igual a cero, deben incluirse como soluciones. Así las soluciones son los
números de la unión de  .
.
Comenzamos con reescribir la inecuación poniendo todos los términos diferentes de 0 al mismo lado:
Factorizando nos da (3x-5)(x+2)<0
En el diagrama de signos.
Vemos
que las soluciones son los números del intervalo abierto  .
.
Inecuaciones racionales
Una inecuación racional es una inecuación que está constituida por el cociente de dos polinomios, tales como.
Para resolver una inecuación racional, encontramos muy útiles las siguientes propiedades adicionales de los números reales.
Propiedad de los signos de los cocientes
3. Si el cociente de dos números reales es positivo, entonces los dos números tienen los mismos signos.
4. Si el cociente de dos números reales es negativo, entonces los dos números tienen signos opuestos.
Ejemplos
Para utilizar las propiedades de los signos (3) y (4), debemos tener todos los términos diferentes de cero al mismo lado de la inecuación. Así, agregamos 1 en ambos lados de la inecuación y luego combinamos términos para obtener una ecuación racional equivalente:
Utilizando el hecho de que 2x + 4 = 0 cuando x = -2 y x + 2 = 0 cuando x = -3.
Realizamos la gráfica de signos.
En esta gráfica podemos ver que
Para
x en  .
El número critico –3 no es la solución, puesto que (2x + 4)/(x + 3) no está
definido para x = -3, pero el denominador critico -2 si, ya que (2x + 4)/(x +
3) es cero para x = -2.
.
El número critico –3 no es la solución, puesto que (2x + 4)/(x + 3) no está
definido para x = -3, pero el denominador critico -2 si, ya que (2x + 4)/(x +
3) es cero para x = -2.
Ya
que todos los términos diferente de cero están a un lado de la inecuación,
comenzamos por dibujar un diagrama de signos con los números críticos -2, 0 y 1.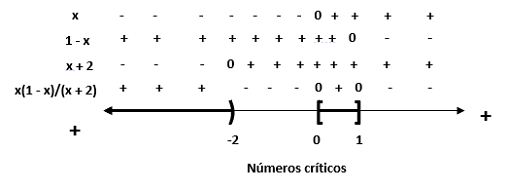
El diagrama muestra que el factor 1 – x es positivo para x < 1 y negativo para x > 1. Notamos también que x (1 - x)/(x + 2) es indefinido para x = -2.
Entonces,
como se indica en la figura, las soluciones están dadas por 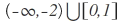 .
.
















No hay comentarios.:
Publicar un comentario