PROPOSICIÓN
Es la expresión verbal o escrita de un pensamiento en el cual se afirma o niega algo.
AXIOMAS PRINCIPALES
1.- Propiedad reflexiva de la igualdad.
a = a
2.- propiedad simétrica de la igualdad.
Si a = b entonces b = a
3.- propiedad transitiva de la igualdad.
Si a = b y b = c entonces a = c
4.- A los dos miembros de la igualdad se pueden sumar, restar, multiplicar, dividir, elevar a una misma potencia o extraer una misma raíz manteniéndose la igualdad.
Si a = b entonces: a + c = b + c
a - c = b - c
a . c = b . c
a/c = b/c
5.- el todo es mayor de cualquiera de sus partes e igual a la suma de las mismas. Este enunciado se conoce como Axioma de la desigualdad.
6.- Propiedad transitiva de la desigualdad.
Si a > b y b > c entonces a > c
Si a < b y b < c entonces a < c
7.- Si a los dos miembros de una desigualdad se multiplican por los números positivos iguales entonces el sentido de la desigualdad se mantiene.
Si d > 0 y a < b entonces a . d < b . d
8.- Si se multiplican los dos lados de una desigualdad por un número negativo el sentido de la desigualdad cambia.
Si d < 0 y c > a entonces c . d < d . a
9.- Si se suman desigualdades del mismo sentido se obtiene otra desigualdad en el mismo sentido.
Si a > b y c > d entonces a + c > b + d
10.- Si se tiene una igualdad y una desigualdad.
Si a = b y p > q entonces a + p > b + d
Si a = b y p > q entonces a - p < b - d
POSTULADOS PRINCIPALES
1.- Existen infinitos números de puntos.
2.- Dos puntos determinan una recta y solo una.
3.- Toda recta puede prolongarse en sus dos sentidos naturales.
4.- Siempre es posible trazar una circunferencia con centros y radios dados.
5.- Toda figura puede ser cambiada de posición sin cambiar de forma y tamaño.
TEOREMAS
Son proposiciones compuestas del tipo
A la posición H se le conoce como hipótesis y representa las condiciones dadas del teorema.
La hipótesis es siempre verdadera. La proposición T se llama tesis y representa una afirmación que para su aceptada debe ser demostrada y por lo general es verdadera.
Ejemplo:
Si dos ángulos son opuestos por el vértice, entonces son congruentes.
La linea del centro de dos circunferencias secantes, es mediatriz de la cuerda común. H T
TEOREMA RECIPROCO (T.R.).- Es el teorema que tiene por hipótesis y tesis, la tesis y la hipótesis del directo, respectivamente.
TEOREMA CONTRARIO (T.C.).- Es aquel que tiene por hipótesis y tesis las negaciones respectivas de la hipótesis y tesis del directo.
TEOREMA CONTRARECIPROCO (T.C.R.).- Es aquel que tiene por hipótesis y tesis las negaciones respectivas de la hipótesis y tesis del recíproco.
Ejemplo:
T.D. Si dos ángulos son opuestos por el vértice entonces son congruentes.
T.R. Si dos ángulos son congruentes entonces son opuestos por el vértice.
T.C. Si dos ángulos no son congruentes por el vértice entonces no son congruentes.
T.C.R. Si dos ángulos no son congruentes entonces no son opuestos por el vértice.
COROLARIOS
Son proposiciones consecuencias inmediatas de un teorema que se aceptan sin demostración, pero que son demostrables.
PROBLEMA (Ejercicio).- Son proposiciones en los que a partir de ciertos datos se debe llegar a ciertos resultados. Dependiendo del tipo de datos que se tenga y de los resultados que se obtengan, los problemas se clasifican en:
1.- Datos : gráficos Resultados: gráficos
Ejemplo:
2.- Datos : gráficos Resultados: numéricos
Ejemplo:
3.- Datos : numéricos Resultados: Gráficos
Ejemplo.
4.- Datos : numéricos Resultados: numéricos
Ejemplo:
Dado el lado , encontrar el área de un cuadrado
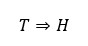
No hay comentarios.:
Publicar un comentario