Es la operación que tiene la finalidad transformar una expresión algebraica racional entera en otra equivalente, que sea igual al producto de sus factores primos racionales enteros. En general, factorizar significa convertir una suma algebraica en un producto de factores.
MÉTODOS PARA FACTORIZAR
1) FACTOR COMÚN
De dos o más expresiones algebraicas, es la parte numérica y/o literal que este repetida en dichas expresiones. El factor común puede ser de tres tipos:
1) Factor común monomio
2) Factor común polinomio
3) Factor común por agrupación
1.1 FACTOR COMÚN MONOMIO
Cuando el factor común de todos los términos del polinomio es un monomio.
Ejemplo:
Factorizar
Para sacar el factor común monomio:
en primer lugar se saca el coeficiente común (24) a continuación, se saca las letras comunes afectadas por los menores exponentes 
,
luego se divide cada término del polinomio entre el factor común monomio y los resultados se escriben dentro del paréntesis.
1.2 FACTOR COMÚN POLINOMIO
Cuando el factor común que aparece es un polinomio
Ejemplo:
Factorizar
efectuando:
luego:
1.3) FACTOR COMÚN POR AGRUPACIÓN
Cuando no hay un factor común a todos los términos del polinomio.
Ejemplo:
Factorizar
efectuando las operaciones:
No hay factor monomio ni polinomio, por lo tanto se agrupa términos de 2 en 2.
Sacando factores comunes en cada paréntesis.
Sacando factores común binomio.
Ejemplo.
Factorizar.
Solución.
Extrayendo factor común: (x+1)
Efectuando
2) MÉTODO DE IDENTIDADES
2.1) DIFERENCIA DE CUADRADOS
Es una diferencia de dos cuadrados perfectos.
Para factorizar, se extrae la raíz cuadrada de los cuadrados perfectos y se forma una suma de las raíces multiplicada por la diferencia de ellas. En general:
2.2) TRINOMIO CUADRADO PERFECTO
Se caracteriza por:
1) Tener dos términos que son cuadrados perfectos.
2) El otro termino es el doble del producto de las raíces cuadradas de los cuadrados perfectos.
3) Los cuadrados perfectos siempre deben tener signo positivo.
El trinomio de estos caracteres se reduce a un binomio al cuadrado así:
2.3) SUMA O DIFERENCIA DE CUBOS
Se caracteriza por tener dos cubos perfectos. Para factorizar se recuerda el producto notable, así:
FACTORIZAR
Solución.
Se puede escribir como:
Factorizando el trinomio cuadrado perfecto:
3) MÉTODO DEL ASPA
3.1) ASPA SIMPLE
Se utiliza para trinomios de la forma:
Para factorizar, se descompone en dos factores los términos
según sea el caso. Se coloca estos factores en las puntas de la izquierda de la aspa. El término independiente, incluyendo el signo también se descompone en dos factores, los cuales se coloca en las puntas de la derecha del aspa. El termino central del trinomio debe ser igual a la suma de los productos del aspa. Por ultimo los factores de la nueva expresión son las sumas en forma horizontal de los extremos del aspa.
Ejemplo.
Factorizar
a)
se descompone en dos factores:
b) 12 también se descompone en dos factores:
Se pone estos factores en los extremos izquierdo y derecho del aspa respectivamente.
c) La suma de los productos.
Es igual al término central.
Nótese que la fracción factorizada es el producto de la suma, tomada horizontalmente, así:
Ejemplo.
Factorizar:
Solución.
Extrayendo factor común:
Aplicando aspa simple al paréntesis, donde:
La expresión propuesta factorizada será:
3.2) ASPA DOBLE
Se aplica para factorizar polinomios de la forma:
Y también para algunos polinomios de cuarto grado.
Procedimiento.
Primero se ordena convenientemente; es decir en forma decreciente para una de las variables, luego se traza y ejecuta un aspa simple para los tres primeros términos con rayas continuas o llenas. A continuación, y pegada a este aspa, se traza otra de tal modo que el producto de los elementos del extremo derecho de este aspa-multiplicados verticalmente sea el término independiente.
Finalmente: primer factor es la suma de los elementos tomados horizontalmente de la parte superior; el segundo factor es la suma de los elementos horizontalmente de la parte inferior.
Ejemplo.
Factorizar:
Explicación.
1) A los 3 primeros términos se les aplica un aspa simple (I):
se verifica (I):
2) A los términos 3°, 4° y 6°, se les aplica un aspa simple (II):
se verifica (II):
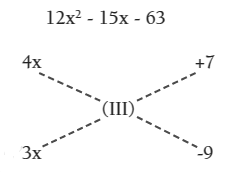
3) A los términos 1°, 5° y 6° se le aplica un aspa simple (III):
se verifica (III):
Luego la respuesta factorizada es:
Ejemplo.
Factorizar:
Verificando los términos:
La expresión factorizada es:
3.3) ASPA DOBLE ESPECIAL
Se utiliza para factorizar polinomios de cuarto grado de la forma general:
Para factorizar se procede así:
a) Se descompone los términos extremos (primero y quinto) en sus factores primos con signos adecuados.
b) Se efectúa el producto de los factores primos en aspa y se reduce. De una manera se obtiene un termino de 2° grado.
c) A este resultado se lo debe sumar algebraicamente otro termino de 2° grado para que sea igual al tercer termino.
d) Con este otro termino de 2° grado colocado como tercer termino del polinomio, se descompone en sus factores en forma conveniente tal, que cumpla los requisitos del aspa doble:
- Aspa simple entre el primer término y el término de 2° grado ubicado como sustituto, para verificar el segundo término.
- Aspa simple auxiliar entre el sumando de 2° grado ubicado y el 5° término para verificar el 4° término.
e) Los factores se toman en forma horizontal.
Ejemplo.
Factorizar.
Solución.
Descomponiendo los extremos en sus factores:
Para (I):
Como el tercer término es
y el producto en aspa de los extremos es
faltarán
que es la cantidad que se debe agregar.
Se descompone
en sus factores en forma conveniente y se verifica el 2° y 4° términos:
Como verificar las condiciones del aspa doble, los términos están bien descompuestos.
La expresión factorizada es:
Ejemplo.
Factorizar:
Solución.
Descomponiendo los términos extremos:
En el aspa (I):
se observa que faltan.
Luego:
Verificando el aspa doble:
La expresión factorizada es:
4) MÉTODO DE DIVISORES BINOMIOS
FINALIDAD.- Permite la factorización de un polinomio de cualquier grado que acepte factores de primer grado de la forma general:
Por ejemplo: x + 2; 2x + 3
DIVISOR BINOMIO.
Es aquel que siendo de primer grado esta contenido un número entero de veces de un polinomio.
Ejemplo.
Contiene exactamente a (x - 2) ya que si se calcula el resto, éste es igual a cero.
FUNDAMENTO TEÓRICO.
Este método es fundamental en la aplicación del teorema del resto en forma inversa y de la división de Ruffini.
Si P(x): (x-a), da R=0; (x-a) es un divisor de P(x).
Si x=a y R=P(a)=0, por el teorema del resto: x-a=0
∴ x-a es un divisor del polinomio P(x).
CEROS DE UN POLINOMIO
Son todos los valores que puede tomar la variable de un polinomio y que hacen que su valor numérico sea igual a cero.
Ejemplo.
Sea el Polinomio:
Valor numérico para x = 1:
P(1) = 1+3+5-9
P(1) = 0
Por lo tanto el número 1 es un cero del polinomio. Se observa que al obtener un cero del polinomio se obtiene también un divisor binomio que es (x-1).
DETERMINACIÓN DE LOS POSIBLES CEROS DE UN POLINOMIO
1) Cuando el primer coeficiente del polinomio es "1" se toman todos los divisores del término independiente con su doble signo.
Ejemplo.
Sea el polinomio:
2) Cuando el coeficiente del primer término es diferente a "1", se procede como en el caso anterior y además, se considera las fracciones que resultan de dividir todos los divisores del primer coeficiente.
Ejemplo.
Sea el polinomio:
Posibles ceros:
FORMAS DE FACTORIZACIÓN
1) Se determina por lo menos un cero del polinomio.
2) De acuerdo con el cero, se halla el divisor, que es un divisor binomio o factor.
3) El otro factor se determina dividiendo el polinomio entre el divisor obtenido mediante la regla de Ruffini.
OBSERVACIONES
- El número de ceros, está determinado por el grado del polinomio.
- El número de ceros mínimo debe ser tal que, al dividir sucesivamente, por Ruffini, se obtenga un cociente de segundo grado.
Ejemplo.
Factorizar:
Solución.
1) Se determina los posibles ceros del polinomio para valores de:
2) Para x=1, el valor numérico del polinomio es:
Luego (x - 1) es un factor.
3) Dividiendo el polinomio entre el valor obtenido, usando la regla de Ruffini:
De donde se obtiene el cociente:
Que , es el otro factor buscado.
4) Luego el polinomio factorizado es:
y, finalmente podemos convertir a:
Ejemplo.
Factorizar:
Solución:
Para x=1
P(1)=0 ∴ (x - 1) es un factor
Para x=2
P(2)=0 ∴ (x - 2) es otro factor
Dividiendo dos veces por Ruffini:
El otro factor es
el cual se factoriza por el método del aspa
resulta: (x - 3)(x + 2)
5) MÉTODO DE ARTIFICIOS DE CÁLCULO
5.1) REDUCCIÓN A DIFERENCIA DE CUADRADOS.
Este método consiste en transformar una expresión (trinomio en general), a una diferencia de cuadrados, sumando y restando una misma cantidad de tal manera que se complete el trinomio cuadrado perfecto.
Ejemplo.
Factorizar:
Solución.
Analizando el trinomio, se observa que los extremos son cuadrados perfectos, para que sea el desarrollo de una suma al cuadrado, el término intermedio debe ser doble del producto de las raíces de estos términos: es decir, debe ser.
Luego, se observa que le falta
Sumando y restando se obtiene:
El primer paréntesis es el desarrollo de un binomio al cuadrado:
Factorizando la diferencia de cuadrados:
Ejemplo.
Factorizar:
Solución.
Se observa que los extremos son cuadrados perfectos, luego el término intermedio debe ser:
Sumando y restando
Finalizando la diferencia de cuadrados:
5.2) MÉTODOS DE SUMAS Y RESTAS
Consiste en sumar y restar una misma cantidad de tal manera que se forme una suma o diferencia de cubos al mismo tiempo que se presenta el factor.
Algunas veces también se completa el polinomio
Ejemplos.
Factorizar:
Solución.
Primera forma: Completando el polinomio.
Sumando y restando.
agrupando y factorizando así:
finalmente.
Segunda forma: Sumando y restando
:
agrupando y factorizando.
sumando y restando al segundo paréntesis:
Finalmente:
Factorizar:
Solución.
Sumando y restando :
agrupando:
factorizando suma de cubos:
finalmente:
5.3) CAMBIO DE VARIABLE
Consiste en cambiar una variable por otra, de tal manera que se obtenga una forma de factorización más simple.
Ejemplo.
Factorizar:
Solución.
Agrupemos adecuadamente, así:
Haciendo
efectuando:
Es el desarrollo de la suma al cuadrado, por lo que:
Remplazamos "a" por su valor:
Ejemplo.
Factorizar.
Solución.
Efectuando los dos binomios.
Haciendo
Efectuando.
Reduciendo.
Que es el desarrollo de una suma al cuadrado, así:
Remplazando "a" por su valor.
Factorizando por aspa simple el paréntesis:
Luego.
5.4) FACTORIZACIÓN RECÍPROCA
POLINOMIO RECÍPROCO.- Es aquel que se caracteriza porque los coeficientes de los términos equidistantes del centro son iguales.
El polinomio:
Es recíproco siempre y cuando. A=E; B=D
Ejemplos.
PROCEDIMIENTO PARA FACTORIZAR UN POLINOMIO RECÍPROCO
1) Se extrae, como factor común, la parte literal del término central, que al final se debe eliminar.
2) Se realiza el siguiente cambio de variables.
3) Se realiza las operaciones y se factoriza.
4) Se repone los valores asignados a las variables.
Ejemplo.
Factorizar:
Solución.
Extrayendo factor común 
:
Agrupando de la siguiente manera:
Haciendo:
Efectuando:
Aplicamos aspa simple al paréntesis:
Luego:
Remplazamos el valor de "a"
Operando:
Simplificando.
5.5) FACTORIZACIÓN SIMÉTRICA Y ALTERNADA
POLINOMIO SIMÉTRICO.- Se dice que un polinomio es simétrico respecto a sus variables cuando su valor no se altera por el intercambio de cualquier par de ellas y además es homogéneo.
Ejemplo.
Sea el polinomio:
Nótese que la expresión sigue una forma circular o cíclica:
Intercambiando dos cualquiera de sus variables sean éstas "x" o "y", es decir remplazamos a "x" por "y" y a "y" por "x", se tiene:
Ordenando en forma circular:
Se obtiene la misma expresión, entonces la expresión es simétrica.
REPRESENTACIÓN DE EXPRESIONES SIMÉTRICAS
Con dos variables: x, y.
Con tres variables: x, y, z.
PROPIEDAD FUNDAMENTAL DE UN POLINOMIO SIMÉTRICO.- Las operaciones de
un polinomio simétrico son expresiones simétricas dan como resultado también expresiones simétricas.
POLINOMIO ALTERNO.- Se dice que un polinomio es alterno respecto a sus variables, cuando su signo se altera pero no su valor absoluto al intercambiar un par cualquiera de ellas, y es homogéneo.
Ejemplo.
Sea el polinomio:
El polinomio sigue una forma circular o cíclica:
Intercambio "x" e "y", se tiene:
Cambiando de signos:
Por lo tanto, el polinomio es alterno.
PROPIEDADES FUNDAMENTALES DE UN DE UN POLINOMIO ALTERNO
1) No hay expresiones alternas que contengan más de dos variables y sean de primer grado.
2) Generalmente los polinomios alternos son circulares o cíclicos y están escritos en forma de diferencia.
3) El producto de una expresión simétrica por una alterna da como resultado una expresión alterna.
PROPIEDAD DE LOS POLINOMIOS SIMÉTRICOS Y ALTERNOS.
1) Una expresión simétrica o alterna de variables x, y, z, si es divisible entre "x", entonces también será divisible entre "y", y entre "z".
2) Una expresión simétrica o alterna de variables x, y, z, si es divisible entre
entonces también será divisible entre
FACTORIZACIÓN DE UN POLINOMIO SIMÉTRICO Y ALTERNO.
1) Se averigua si el polinomio es simétrico o alterno.
2) Encontrar los factores de la expresión aplicando el Teorema del Resto y ampliarlo aplicando las propiedades del polinomio simétrico y alterno.
3) Calcular el cociente, planteando la identidad de 2 polinomios y aplicando el criterio de los valores numéricos.
Ejemplo.
Factorizar:
Solución.
1) Intercambiando "x" por "y" la expresión es alterna.
2) Cálculo de los factores.
Valor numérico para x = y:
∴ El polinomio es divisible entre (x - y).
Por ser el polinomio alterno, también será divisible entre los factores obtenidos en forma circular en el sentido indicado.
Es decir: ( y - z), (z - x).
∴ El polinomio es divisible entre el producto: (x - y)(y - z)(z - x).
3) Se plantea la identidad de polinomios siguientes:
Por ser el polinomio de tercer grado, Q debe ser de grado cero, es decir debe ser un número:
Probemos un juego de valores para x, y, z.
Para x=1, y=2, z=3:
La expresión factorizada es finalmente:
3(x - y)(y - z)(z - x)
Ejemplo.
Factorizar:
Solución.
1) Intercambiando a por b, el polinomio es alterno.
2) Para a=0:
(no hay factores monomios)
3) Para a=b:
Como se anula, entonces un factor es (a - b), y como es alterno, los otros factores siguen un orden circular, en el sentido indicado, es decir:
4) El polinomio es de cuarto grado y los factores obtenidos dan producto de tercer grado, por lo que se hace falta un polinomio de primer grado simétrico y de tres variables de la forma: M(a + b + c)
Realizando la identidad de polinomios:
Dando valores para a=1, b=0, c=2, se obtiene:
∴ M = 1
Finalmente:
5.6) OTROS ARTIFICIOS
Cualquier otro artificio matemático dependerá del cuidado, ingenio y atención que ponga el operador para introducirla.
Ejemplos.
Factorizar:
Solución.
En este ejercicio, se trata de hallar dos trinomios cuadrados perfectos. Se puede escribir la expresión como:
Factorizando.
Factorizando la licencia de cuadrados.
Finalmente.
Factorizar:
Se trata de obtener dos trinomios cuadrados perfectos, sumando y restando
Factorizando.
Factorizando la diferencia de cuadrados.
Finalmente.
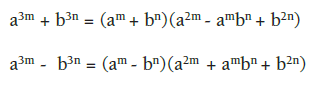
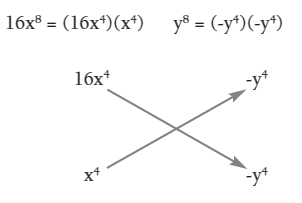
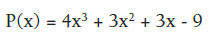
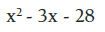
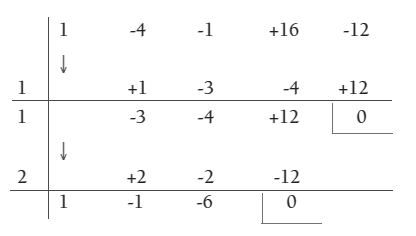
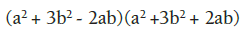
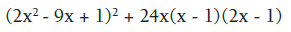
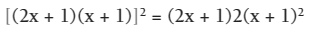
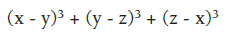
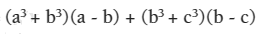
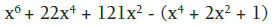
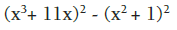
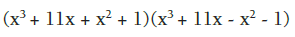
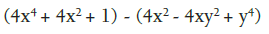
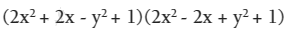
No hay comentarios.:
Publicar un comentario