EXPONENTES ENTEROS
Creemos que es más conveniente escribir una suma repetida X+X+X+X de forma 4X. De igual forma, podemos escribir el producto X . X . X = $X^{3}$. En general, para cualquier número real X y para cualquier entero positivo n, el símbolo $X^{n}$, que se lee como “X a la enésima potencia”, representa el producto de n factores de X. así.
Para cualquier entero positivo n. en la expresión $X^{n}$, n se denomina exponente o potencia de X y X se denomina base. Por ejemplo,
Finalmente, para cualquier base X diferente de cero, definimos
$$X^{0}=1$$
Entonces, $X^{0}=1$
$\left ( \sqrt{2}+\sqrt{3} \right )^{0}=1$
Notemos que $0^{0}$ es indefinido.
NOTA DE ADVERTENCIA: es importante reconocer la diferencia entre 5x3 Y (5x)3 se aplica a 5X y no se aplica a 5X y no sólo a X. En otras palabras.
$7x^{3}$ = 4.X.X.X
$(7x)^{3}$ = 7X.7X.7X = $343x^{3}$
De igual forma.
$-6^{4}$ = -(6.6.6.6) = -1296
$(-6)^{4}$ = (-6) (-6) (-6) (-6) =1296
LEYES DE LOS EXPONENTES
Se han establecido varias reglas para combinar potencias llamadas leyes de exponentes. Como ejemplo simple, consideremos el producto $4^{3}\cdot 4^{5}$, al contar los factores observamos que.$=4^{8}=4^{3+5}$
En general, si la X es cualquier número y m y n son enteros positivos, entonces.
Cuando tanto m como n son negativos, los factores se cuentan de la misma forma, aunque estén en el denominador de la fracción resultante si $m\geq 0$ y n es negativo, tenemos que n = -q donde q > 0. Entonces.
Después de todos los factores disponibles posibles han sido cancelados, bien quedan en el numerador m – q factores o q – m factores en el denominador.
En el primer caso.
$$X^{m} X^{n} = X^{m} X^{-q} = X^{m-q} = X^{m+n}$$
Y en el segundo caso.
Por un argumento similar, puede verificarse que $X^{m}\cdot X^{n} = X^{m+n}$ si m es negativo y $n\geq 0$.
Esta y otras fórmulas que involucran a los exponentes están en la lista a continuación.
LEYES DE LOS EXPONENTES ENTEROS
Sean X y Y números reales y m y n números enteros. Entonces.
Dado que cada expresión representa un número real.
Ejemplos.
EXPONENTES RACIONALES
El concepto de raíz enésima de un número nos capacita para ampliar la definición de $X^{n}$ de exponentes enteros a exponentes racionales, con frecuencia es más fácil trabajar con exponentes racionales que con radicales.
Para cualquier número real X y para cualquier entero positivo n, definimos
Dado que $\sqrt[n]{X}$ sea un número real. Así, $X^{\frac{1}{n}}$ es simplemente otra forma de designar la raíz enésima principal de X. además definimos
Para cualquier entero m tal que m/n sea la mínima expresión. Se necesita esta última definición si la ley de exponentes $(X^{r})^{s} = X^{rs}$ va aplicar a exponentes racionales.
Para X>0, se puede demostrar que
Sin embargo, para X<0 y ciertas opciones de m y n, $X^{1/n}$ no es un número real y en consecuencia, $(X^{1/n})^{m}$ no está definida, aunque la expresión $(X^{m})^{1/n}$ podría estar definida.
De otra parte si, $X^{m/n}$, $(X^{1/n})^{m}$, y $(X^{m})^{1/n}$ cada uno representa un número real, entonces todos son iguales.
LEYES DE LOS EXPONENTES RACIONALES
Las leyes de los exponentes que se dieron para los exponentes enteros, también son verdaderas para los exponentes racionales.
Sean X y Y números reales y s y r números racionales. Entonces.
Ejemplos.
La evaluación de:















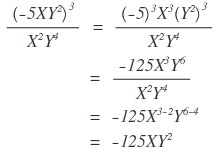














No hay comentarios.:
Publicar un comentario