Se denomina ángulo a la sección del plano que queda comprendida entre dos semirrectas que se que se originan en un mismo punto, y están colocadas en distintas direcciones. El punto en que se inician las semirrectas se denomina vértice del ángulo; en tanto que cada una de las semirrectas que lo delimitan, se denominan lados del ángulo.
Se define que un ángulo es positivo cuando se mide en el sentido contrario a las agujas del reloj (también llamado sentido antihorario, sentido levógiro o sentido directo), y por lo tanto es negativo si se mide en sentido contrario, es decir, en el mismo sentido que las agujas del reloj (sentido horario, sentido dextrógiro o indirecto). En un sistema de ejes cartesianos, se toma por convención que, los ángulos se miden desde el eje positivo de las abscisas en sentido contrario a las agujas del reloj. En general los ángulos se denotan con letras griegas.
ÁNGULO CONVEXO.
Dados tres puntos no colineales A, B, C, Se define como ángulo convexo ABC, se le denota por $\widehat{ABC}$, $\measuredangle ABC$, $\measuredangle B$ o $\widehat{B}$, como la intersección del semiplano de
que contiene a C con el semiplano de borde
que contiene a A.
ELEMENTOS DEL ÁNGULO CONVEXO
Lados del ángulo. Son los rayos $(\overrightarrow{BC}\, \, y\,\, \overrightarrow{BA})$ que tienen el mismo origen.
Interior del ángulo.
Exterior del ángulo.
ÁNGULO CÓNCAVO.
Dados tres puntos no colineales P, Q y R; se define al ángulo $\widehat{PQR}$ cóncavo, con la unión del semiplano del borde $\overrightarrow{PQ}$ que no contiene a R, con el semiplano de borde $\overrightarrow{QR}$ que no contiene a P.
MEDIDA DE LOS ÁNGULOS.
Es el número de veces que un ángulo unitario arbitrario está contenido en un ángulo determinado. dependiendo de la unidad angular tomada, existen 3 sistemas fundamentales de medida angular: sexagesimal, centesimal y circular.
a) SISTEMA SEXAGESIMAL.
Se llama grado (°) a cada uno de los 360 partes en las que se divide el círculo a partir de su centro (O).
b) SISTEMA CENTESIMAL.
Se llama grado centesimal (g) a cada una de las 400 partes en las que se divide un círculo a partir de de su centro (O).
c) SISTEMA CIRCULAR.
La unidad de medida de este sistema es el radián (rad). Un radián es la medida de un ángulo central cuyos lados intersecan un arco de circunferencia (S) de longitud igual al radio (R).
ÁNGULOS CONGRUENTES.
Dos ángulos son congruentes si y solo si tienen la misma medida.
BISECTRIZ DE UN ÁNGULO.
Es el rayo interior que lo divide en dos ángulos congruentes.
Todos los ángulos en geometría se consideran positivos siempre.
CLASIFICACIÓN DE LOS ÁNGULOS
1) Ángulo agudo.- Si su medida es menor a 90°
2) Ángulo Recto.- Si su medida es igual a 90°
Se lo representa así.
3) Ángulo Obtuso.- Si su medida es mayor que 90° y menor que 180°
4) Ángulo Llano.- Es un semiplano; cualquier punto de la frontera se considera vértice del ángulo y su medida es 180°.
5) Ángulos Consecutivos.- Son dos o más ángulos que tiene el mismo vértice y comparten un lado.
6) Ángulos Complementarios.- Son dos ángulos cuya suma de medidas es igual a 90°.
7) Ángulos Suplementarios.- Dos ángulos son suplementarios si y sólo si la suma de sus medidas es igual a 180°.
8) Ángulos Adyacentes.- Son ángulos consecutivos y suplementarios.
9) Ángulos Conjugados.- Son dos ángulos cuya suma de medida es igual a 360°.
10) Ángulos determinados por dos rectas intersecadas por una transversal.
Ángulos Internos: 3,4,5 y 6
Ángulos Externos: 1,2,7 y 7
Ángulos Alternos Internos: 4 y 6; 3 y 5
Ángulos Alternos Externos: 1 y 7; 2 y 8
Ángulos Correspondientes: 1 y 5; 2 y 6; 3 y 7; 4 y 8
Ángulos Colaterales Internos: 4 y 5; 3 y 6
Ángulos Colaterales Externos: 1 y 8; 2 y 7
11) Ángulos opuesto por el vértice.- Son los ángulos que se forman cuando dos rectas se intersecan y tienen los lados mutuamente opuestos.
RECTAS PERPENDICULARES
Dos rectas son perpendiculares si se intersecan formando un ángulo de 90°.
PROPOSICIONES DE PERPENDICULARIDAD.
1.- Desde un punto exterior a una recta es posible construir una y sólo una perpendicular.
H pie de la perpendicular
2.- En un punto cualquiera de una recta se puede construir una y solo una sólo una perpendicular a dicha recta.
Distancia desde un punto exterior a una recta.- Es la longitud del segmento perpendicular trazado desde el punto exterior a la recta.
Mediatriz de un segmento (mz).- Es la perpendicular levantada desde el punto medio del segmento.
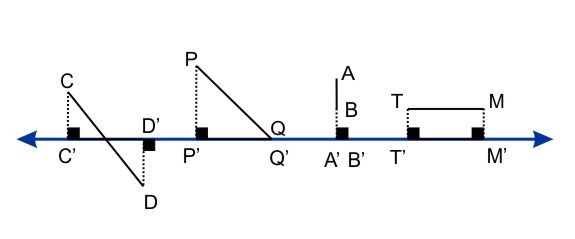
Proyección de un punto sobre una recta.- Es el pie de la perpendicular trazada desde el punto a la recta.
Proyección de un segmento sobre una recta.- Es el segmento de la recta determinado por las proyecciones de los extremos del segmento.
Ejemplos.
POSTULADO DEL PARALELISMO
1.- Dos rectas son paralelas si y solo si la suma de las medidas de los ángulos colaterales internos de un mismo lado de una transversal es igual a 180°.
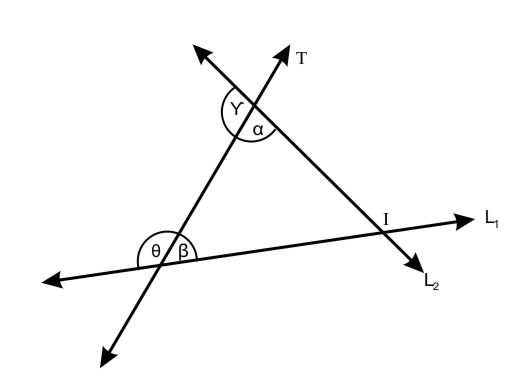
2.- Dos rectas se intersecarán o cortaran si o solo si la suma de las medidas de los ángulos colaterales internos de un mismo lado de una transversal no es igual a 180°. Las rectas se intersecarán en el semiplano en que la suma de las medidas de los ángulos colaterales internos sea menor a 180°.
TEOREMAS BÁSICOS DE ÁNGULOS.
Teorema 1.- Dos ángulos opuestos por el vértice son congruentes.
D)
Teorema 2.- Los ángulos alternos internos, alternos externos y correspondientes, determinados por dos rectas paralelas cortadas por una transversal, son congruentes.
D)
Teorema 3.- Las bisectrices de dos ángulos adyacentes son perpendiculares entre si.
D)
Teorema 4.- Las bisectrices de dos ángulos opuestos por el vértice son colineales.
Teorema 5.- Dos ángulos que tienen respectivamente sus lados paralelos son congruentes o suplementarios.
Teorema 6.- Dos ángulos que tienen respectivamente perpendiculares sus lados son congruentes o suplementarios.
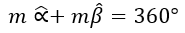
No hay comentarios.:
Publicar un comentario