DEFINICIÓN.
Dados tres puntos no colineales A, B, C, se define al triángulo ABC que se denota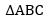



El triángulo se nota con las letras mayúsculas ubicadas cerca de los vértices siguiendo un sentido horario, en lo posible.
ELEMENTOS DE UN TRIÁNGULO
Vértices.- Son los puntos no colineales: A, B y C.
Lados.- Son los segmentos determinados por los vértices:
Ángulos internos.- Son los ángulos convexos formados al interior del triángulo:
Ángulos externos.- Son los ángulos adyacentes a los internos:
Perímetro (P).- Es la suma de las longitudes de los lados:
P = a + b + c ó AB + BC + AC =P
Semiperímetro (p).- Es la semisuma de las longitudes de los lados
CLASIFICACIÓN
Por sus lados:
Escaleno.- Si no tiene ninguno de sus lados congruentes.
Isósceles.- Si tiene un par de lados congruentes.
Equilátero.- Si tiene sus tres lados congruentes.
Por sus ángulos:
Rectángulo.- Si tiene un ángulo recto.
Acutángulo.- Si tiene sus ángulos agudos.
Obtusángulo.- Si tiene un ángulo obtuso.
Equiángulo.- Si tiene sus tres ángulos congruentes.
PUNTOS Y LÍNEAS FUNDAMENTALES DEL TRIÁNGULO
Mediana.- Es el segmento que tiene por extremos un vértice cualquiera del triángulo y el punto medio del lado opuesto, por tanto cualquier triángulo tendrá siempre 3 medianas:
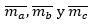
El triángulo
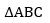
Las tres medianas de un triángulo se intersecan en un único punto G. llamado BARICENTRO o centro de gravedad del triángulo, punto que esta ubicado en la parte interior de cualquier parte clase de triángulo.
Bisectriz interna (o bisectriz de un triángulo).- es el segmento que tiene un extremo un vértice cualquiera del triángulo y el punto de intersección de la bisectriz de ese ángulo interno con el correspondiente lado opuesto.
Existirán entonces tres bisectrices internas en cualquier triángulo:, respectivamente.
Las bisectrices internas de un triángulo cualquiera se intersecan en un punto I llamado INCENTRO o centro de la circunferencia inscrita en dicho triángulo. El punto I está ubicado siempre en la parte interior del triángulo cualquier triángulo.
Bisectriz interna de un triángulo.- Es el segmento que tiene por extremos un vértice cualquiera de un triángulo y el punto de intersección de la bisectriz de ese ángulo externo con la prolongación del correspondiente lado opuesto.
De acuerdo al postulado de paralelismo se tiene que:
- Un triángulo escaleno tiene 3 bisectrices externas.
- Un triángulo isósceles tiene solamente 2 bisectrices externas.
- Un triángulo equilátero no tiene bisectrices externas.
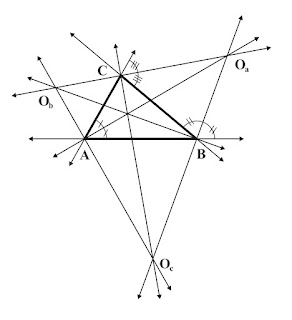
Excentros.- Son los puntos de intersección de dos bisectrices de ángulos externos que se encuentran en un mismo semiplano respecto a un lado de un triángulo y la bisectriz del ángulo interno opuesto a dicho lado.
Uniendo los puntos 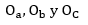
Altura.- Es el segmento perpendicular trazado desde un vértice cualquiera al lado opuesto o a su prolongación. Cualquier triángulo tiene 3 alturas:
El
Las 3 alturas se intersecan en un único punto H llamado ORTOCENTRO, punto que está ubicado al interior del triángulo si este es acutángulo y en el exterior del mismo si este es obtusángulo, en este caso el ortocentro se determina prolongando las alturas.
Mediatriz.- Es la recta perpendicular levantada en el punto medio de un lado cualquiera del triángulo tiene 3 mediatrices:
Las 3 mediatrices se intersecan en un único punto O llamado CIRCUNCENTRO, el mismo que se encontrará dentro del triángulo si es acutángulo, y fuera de él, si es obtusángulo.
El CIRCUNCENTRO es el centro de la circunferencia circunscrita al triángulo y que pasa por los 3 vértices del mismo.
Base.- Es cualquier lado de un triángulo, por lo tanto todo triángulo tiene 3 bases. En el caso del triángulo isósceles se acostumbra llamar base al lado no congruente.
TEOREMAS
Teorema 1.- La suma de las medidas de los ángulos internos de un triángulo es igual a 180°.
D)
- Un triángulo no puede tener más de un ángulo recto u obtuso.
- La medida de un ángulo es igual a la suma de las medidas de los ángulos internos no adyacentes.
- En un triángulo rectángulo los ángulos agudos son complementarios.
- En un triángulo equiángulo cada uno de los ángulos mide 60°.
Ejercicio:
D)
Dos triángulos son congruentes si y solo si tienen respectivamente congruentes sus tres lados y sus tres ángulos.
Postulados de Congruencia.
1. Dos triángulos son congruentes si tienen respectivamente congruentes los lados y el ángulo comprendido entre ellos. A este postulado se le conoce como criterio de congruencia lado, ángulo, lado, que se representa como L.A.L.
2. Si dos triángulos tienen respectivamente congruentes dos ángulos y un lado homólogo cualquiera entonces son congruentes. A este criterio se le conoce como ángulo, ángulo, lado, que se le representa como A.A.L.
3. Si dos triángulos tienen respectivamente congruentes sus 3 lados entonces son congruentes. A este criterio se le conoce como lado, lado, lado, que se le representa como L.L.L.
Teoremas referentes al Triángulo Isósceles.
Teorema 2.- En un triángulo isósceles, a los lados congruentes se oponen ángulos congruentes.
D)
Corolarios.
- Los ángulos en la base de un triángulo isósceles son congruentes.
- Si un triángulo tiene dos ángulos congruentes entonces los lados que se oponen a dichos ángulos son congruentes.
- Un triángulo es equilátero si y sólo si es equiángulo.
- Si un triángulo se tiene que una altura es mediana al mismo tiempo; altura y bisectriz o mediana y bisectriz entonces el triángulo es isósceles.
- En un triángulo isósceles se tiene que la altura relativa a la base es simultáneamente mediana y bisectriz.
- En un triángulo equilátero, la altura, mediana y bisectriz interna coinciden respecto a un mismo vértice, por lo tanto también coinciden el ortocentro, baricentro y el incentro.
Teorema 3.- Todo triángulo isósceles tiene:
i) Dos bisectrices laterales congruentes.
ii) Dos alturas laterales congruentes y
iii) Dos medianas laterales congruentes.
i)
D)
ii)
iii)
Corolario.
En un triángulo equilátero, las medianas, alturas, y bisectrices relativas a los tres lados son congruentes y según el teorema 2, coinciden respecto a un mismo vértice.
Ejercicio.
D)
Teoremas referentes al Triángulo Rectángulo.
Teorema 4.- En un triángulo rectángulo, la mediana relativa a la hipotenusa es congruente con los segmentos que determina en la misma.
Corolario.
El punto medio de la hipotenusa de un triángulo rectángulo equidista de los tres vértices, siendo por lo tanto el circuncentro de dicho triangulo.
Teorema 5.- Si en un triángulo la mediana relativa a una de los lados es congruente con los segmentos que la misma determina en ese lado entonces el triángulo es rectángulo, y el ángulo recto esta ubicado en el vértice desde donde se traza la mediana.





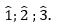







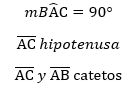



















































No hay comentarios.:
Publicar un comentario