Las matrices se utilizan para describir sistemas de ecuaciones lineales, y registrar los datos que dependen de varios parámetros.
Una matriz es un arreglo rectangular de números dentro de corchetes.
Por ejemplo
los números dentro de los corchetes son los elementos de la matriz.
la matriz de la izquierda tiene 2 renglones y 2 columnas y se llama matriz 2 por 2 (2x3). La matriz de la derecha contiene 2 renglones y 3 columnas y es una matriz 2 por 3 (2x3).
El número de renglones es la primera dimensión que se da, y el número de columnas es la segunda dimensión que se da.
Una matriz cuadrada tiene el mismo número de renglones que de columnas.
Se acostumbra a denotar con una letra mayúscula del abecedario.
A los arreglos horizontales se les denomina renglones o filas.
A los arreglos verticales se les denomina columnas.
Al número (imagen) se lo denomina elemento de la matriz, donde "i" (el primer número del subíndice) indica la fila en donde se encuentra y "j" (el segundo número del subíndice) la columna, es decir:
ORDEN O DIMENSIÓN
El orden o la dimensión de una matriz está dada por la cantidad filas y la cantidad de columnas que posea. Al decir $A_{nxm}$, se indica que A es una matriz que tiene m filas y n columnas.
Ejemplos.
CLASES DE MATRICES
1) MATRIZ CUADRADA
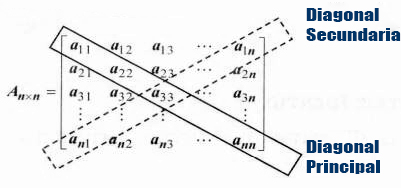
Una matriz cuadrada tiene igual cantidad de filas que de columnas y se le denota como $A_{nxn}$.
Caso contrario se le considera una matriz rectangular.
Cuando una matriz es cuadrada surge la la definición de Diagonal Principal para los elementos $a_{ij}$ donde i=j. Y Diagonal Secundaria para los elementos de la otra diagonal.
La suma de los elementos de la Diagonal Principal se llama Traza de la matriz y se le denota como Tr(A), es decir:
Dentro de las matrices cuadradas también aparecen las siguientes clases de matrices:
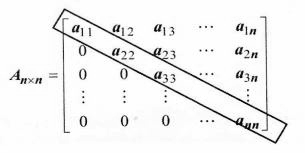
a) MATRIZ TRIANGULAR SUPERIOR.
Una matriz cuadrada es triangular superior cuando los elementos que están bajo la Diagonal principal son todos ceros:
b) MATRIZ TRIANGULAR INFERIOR.
Una matriz cuadrada es triangular inferior cuando los elementos que están sobre la Diagonal principal son todos ceros:
c) MATRIZ DIAGONAL.
Una matriz cuadrada es triangular inferior cuando los elementos que están sobre y debajo la Diagonal principal son todos iguales a cero:
d) MATRIZ IDENTIDAD.
Es una matriz diagonal que tiene el número 1 en toda la Diagonal Principal.
e) MATRIZ CERO.
Es una matriz que tiene todos sus elementos ceros. Puede ser cuadrada como puede ser rectangular.
2) MATRIZ FILA.
Se llama matriz fila a la que sólo tiene una fila, es decir su dimensión es (1xn).
Por ejemplo:
A = [1 -4 0 9]
3) MATRIZ COLUMNA.
Se llama matriz columna a la que sólo consta de una columna, es decir su dimensión será (mx1).
Por ejemplo:
4) MATRIZ RECTANGULAR.
Una matriz es rectangular si no es cuadrada, es decir, tiene diferente número de filas que de columnas.
Por ejemplo:
5) MATRIZ ESCALAR
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
Por ejemplo:
Una matriz es normal si conmuta con su traspuesta, esto es, si $AA^{t}=A^{t}A$. Obviamente, si A es simétrica, anti simétrica u ortogonal, es necesariamente normal.
7) MATRICES ESCALONADAS.
Una matriz es escalonada si al principio de cada fila (o columna) un elemento nulo más que en la fila (o columna ) anterior.
Una matriz regular es una matriz cuadrada que tiene inversa.
9) MATRIZ SINGULAR.
Una matriz singular no tiene matriz inversa.
10) MATRIZ IDEMPOTENTE.
Una matriz, A, es idempotente si:
11) MATRIZ INVOLUTIVA.
Una matriz, A, es involutiva si:
12) MATRICES ANTISIMÉTRICA O HEMISIMÉTRICA.
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica.
13) MATRIZ ORTOGONAL.
Una matriz es ortogonal si verifica que:
14) MATRIZ TRASPUESTA.
Sea $A=(a_{ij})$ una matriz de mxn. Entonces su matiz traspuesta, denota como $A'=(a_{ji})$, es de nxm y se obtiene tomando las filas de la matriz A como columnas para la matriz A' y por ende las columnas de la matriz A serán las filas de la matriz $A^{t}$.
Ejemplo.
La traspuesta de la matriz A es:
PROPIEDADES
Sean $A_{mn}$ y $B_{mn}$ matrices, entonces:
1. (A')' = A
2. (A + B)' = A' + B'
3. (AB)' = B'A'
15) MATRIZ SIMÉTRICA.
Una matriz $A_{nn}$ es simétrica si y sólo si A' = A
Para que una matriz sea simétrica se debe cumplir que $a_{ij}=a_{ji}$.
Ejemplo
16) MATRIZ INVERSA.
Sea A una matriz de nxm. Si existe una matriz $A_{n\times xn}^{-1}$ tal que $AA^{-1}=A^{-1}A=1$, se dice que A es inversible.
En este caso la matriz $A_{n\times n}^{-1}$ se llama la matriz inversa de A.
Si $A^{-1}$ existe, se dice que A es una matriz no singular. Caso contrario; es decir, que $A^{-1}$ no exista, se dice que A es una matriz singular.
Existen varias maneras de calcular la matrices inversas, una de las manera de calcular es por medio de la siguiente fórmula:
Esto da lugar el siguiente teorema (Una condición necesaria y suficiente para la existencia de la matriz inversa)
Teorema.
Si $A^{-1}$ existe si y sólo si $\left | A \right |\neq 0$
PROPIEDADES
Sean $A_{n\times n}$ y $A_{n\times n}$ matrices inversibles, entonces:
Ejercicio
Hallar la inversa de la matriz A:
Primero calculamos el determinante de la matriz A
|A| = -7, este resultado nos indica que si va a existir matriz inversa.
Calculamos la matriz de cofactores.
Comprobando.


























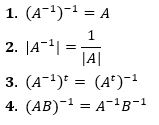




No hay comentarios.:
Publicar un comentario