DEFINICIÓN.
Se define al determinante como una función que asigna un número a toda matriz cuadrada.
El determinante de una matriz, como resultado generará un escalar, el cual representa la singularidad de dicha matriz.
Dada la matriz A, su determinante esta denotado por: det(A) o |A|.
Existen diferentes métodos para hallar el determinante de una matriz, desde los mas sencillos hasta los complejos dependiendo de la longitud de la matriz.
- Regla de SARRUS
- Método de COFACTORES
Procedimiento para calcular el determinante cuadrada 3x3 por la regla de SARRUS.
Dada la siguiente matriz
Se llamará los SUMANDOS POSITIVOS que se obtiene se la siguiente manera:
1) Los elementos de la diagonal principal:
2) Los elementos de la línea paralela superior a la diagonal principal por el elemento aislado de la esquina inferior izquierda:
3) Los elementos de la línea paralela inferior a la diagonal principal por el elemento aislado de la esquina superior derecha:
Representación gráfica
Se llamará los SUMANDOS NEGATIVOS que se obtiene se la siguiente manera:
1) Los elementos de la diagonal secundaria:
2) Los elementos de la línea paralela superior a la diagonal secundaria por el elemento aislado de la esquina inferior derecha:
3) Los elementos de la línea paralela inferior a la diagonal secundaria por el elemento aislado de la esquina superior izquierda:
Representación gráfica.
El resultado del determinante de la matriz A, sería |A|= SUMANDOS POSITIVOS - SUMANDOS NEGATIVOS.
Ejemplo:
Calcular el determinante de la matriz A.
Resolución.
|A| = (-2).7.2+4.(-3).3+6.0.5-(3.7.5+6.4.2+0.(-3).(-2))
|A = -28-36+0-(105+48+0)
|A| = -28-36-153
|A| = -217
Procedimiento para calcular el determinante cuadrada 3x3 por el método de COFACTORES.
Cuando se usa el método de cofactores para el cálculo de un determinante es importante escoger un renglón o una columna con el mayor número de ceros posible. Esto se debe que los cofactores correspondientes a tales elementos cero no hace falta calcularlos.
Sea A una matriz de n x n. El cofactor ij de $A_{j}$ está dada por
Esto es, el cofactor ij de A se obtiene el determinante del menor ij y se multiplicándolo por $(-1)^{i+j}$. observe que
Para hallar los cofactores de una matriz, calculamos primero los menores y, a continuación, aplicamos la siguiente regla: si la suman de la fila + columna del elemento es par, el signo del cofactor es positivo, mientras que será negativo si la suma es impar.
Sea la matriz A calcular su determinante por cofactores.
Entonces.
Ejemplo
Evalúe el determinante de la siguiente matriz
Solución
PROPIEDADES DE LOS DETERMINANTES
1) Si cada elemento de cualquier renglón (o columna) de un determinante se multiplica por una constante k, el nuevo determinante es k veces el original.
2) Si dos renglones (o columnas) de un determinante se intercambian, el nuevo determinante es el negativo al original.
3) Si los elementos correspondientes son iguales en dos renglones (o columnas), el valor del determinante es 0.
4) Si cada elemento de un renglón (o columna) es 0, el valor del determinante es 0.
6) Si una matriz es triangular superior, triangular inferior o diagonal, entonces su determinante es igual a la multiplicación de los elementos de la diagonal principal.
7) Si en un determinante una línea (fila o columna) está descompuesta en sumas, podemos descomponer el determinante en suma de determinantes.
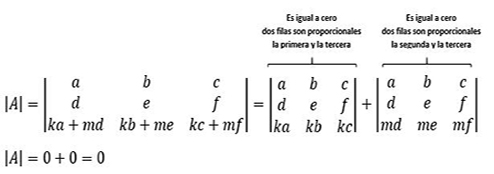
8) Si a una línea le sumamos otra línea paralela multiplicada por una constante, el determinante no varía.
A la primera fila le sumamos la segunda multiplicada por k, es decir:
vemos que el determinante no varia.
9) Si un determinante tiene una línea (fila o columna) que es combinación lineal de otras líneas paralelas, el determinante es cero, y también recíprocamente si el determinante de una matriz es cero entonces una fila (y una columna) es combinación lineal de las demás.
vemos que el determinante no varia.
10) El determinante de un producto de dos matrices es igual al producto de sus determinantes.
11) El determinante de una matriz es igual al de su traspuesta.
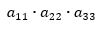
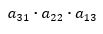
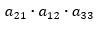
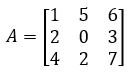
No hay comentarios.:
Publicar un comentario