El mecanismo que consiste en determinar la máxima cantidad de figuras, de cierto tipo, que se encuentran presentes en una figura dada.
MÉTODOS DE CONTEO
A) CONTEO DIRECTO:
1) MÉTODO DE SCHOENK.
consiste en asignar números y/o letras a todas las figuras simples, posteriormente al conteo creciente y ordenado, de figuras de 1 número, al unir 2 números, al unir 3 números.... etc.
Ejemplo.
¿Cuántos cuadriláteros hay en?
Resolución:
Cuadriláteros de 1 número: ninguno.
Cuadriláteros de 2 número: 12, 23, 34, 45, 56, 61 = 6
Cuadriláteros de 3 número: 123, 234, 345, 456, 561, 612 = 6
Total de cuadriláteros = 12
B) CONTEO MEDIANTE INDUCCIÓN (FÓRMULA)
Consiste en analizar casos particulares a la figura dada (figuras análogas), tratando de encontrar una ley de formación coherente para luego poder generalizar (Encontrar la formula).
Ejemplo.
Cuántos cuadriláteros hay en:
Resolución:
Casos particulares:
Para n=1
Para n=2
Para n=3
La figura será.
Ley de la formación.
1 (Para 1 espacios)
1+2 (Para 2 espacios)
1+2+3 (Para 3 espacios)
Luego: Para "n" espacios:
Número de triángulos.
entonces para 2 espacios será.
Existen 210 triángulos en la figura propuesta.
Nota:
Este método nos sirve para contar también "segmentos", "cuadriláteros", "ángulos agudos", "sectores circulares" "hexágonos", "trapecios", "letras", etc.
2) MÉTODO PRÁCTICO.
El número de figuras está dado por la mitad de la multiplicación de números de espacios y el consecutivo del número de espacios.
Ejemplos.
Cuántos triángulos hay en:
Resolución.
Método práctico
Cuántos segmentos hay en:
Resolución.
Método práctico
Cuántos cuadriláteros hay en:
Resolución.
Método práctico
Cuántos ángulos agudos hay:
Resolución.
Método práctico
Cuántos sectores circulares hay en:
Resolución.
Método práctico
Cuántos hexágonos hay en:
Resolución.
Analizando casos particulares nos daremos cuenta que cumple con el método práctico.
Cuántos cuadriláteros hay en:
Resolución.
Contando directamente encontramos 18. pero el método mas rápido sería:
EN GENERAL:
Cuántos cuadriláteros hay en:
Resolución.
Método práctico
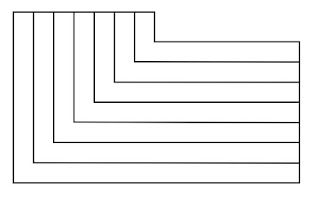
Cuántos paralelepípedos hay:
Resolución.
Método práctico
3) CONTEO DE CAMINOS
Ejemplos.
De cuántas maneras se puede leer la palabra "PELOTA".
Resolución.
Triángulo de Pascal
La palabra "PELOTA" se puede leer de 32 formas.
De cuántas maneras se puede leer la palabra "CONEJOS".
Resolución.
Triángulo de Pascal
Se puede leer de 20 maneras.
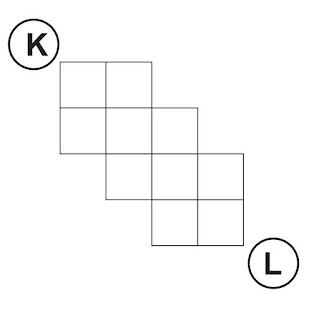
De cuántas formas se puede ir de "K" a "L" sin retroceder.
Resolución.
Triángulo de Pascal
Se puede ir de 54 formas "K" a la "L".
De cuántas formas se puede ir desde "A" hasta "B" por el camino más corto.
Resolución.
Se puede hacer el recorrido de 35 formas diferentes.



































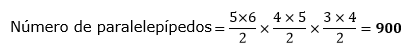







No hay comentarios.:
Publicar un comentario