La teoría de conjuntos es un sistema que emplea un lenguaje matemático muy específico para dar solución a determinado tipo de problemas.
Los conjuntos se han empleado para enseñar a contar y resolver problemas que incluyen la noción de cantidad, esto nos lleva a comprender el concepto de número entero con mayor facilidad y las ideas geométricas al emplear la teoría de conjuntos.
CONJUNTO.
Se le llama conjunto a una colección o agrupación de elementos perfectamente bien definidos y diferenciados dentro de un todo.
Por ejemplo.
Hablaremos de una colección de arte.
Un grupo de estudiantes.
REQUISITOS PARA FORMAR UN CONJUNTO
a) A los elementos hay que agruparlos o coleccionarlos de una manera bien definida.
b) Ningún elemento del conjunto se debe contar más de una vez, si un elemento se repite se debe quitar (todos los elementos deben ser distintos).
c) El orden en que se enlistan los elementos no tiene importancia.
REPRESENTACIÓN DE CONJUNTOS
a) En general a un conjunto se le asigna cualquier nombre o se denotan con las letras mayúsculas del abecedario (A, B, C, ... etc.).
b) Los elementos de un conjunto se colocan entre llaves { } y separados por comas, ejemplo: {1, 2, 3, 4, 5, 6, 7, 8, 9}.
c) Los elementos de los conjuntos se representan con símbolos numéricos, letras minúsculas del abecedario y la combinación de los dos anteriores, por ejemplo:
c.1 A={1, 2, 3, 4, 5, 6, 7, 8, 9, 0}
c.2 B={a, e ,i, o, u}
c.3 C={casa, 4x, 2b, 3*}
d) La representación gráfica es a través de los diagramas de Venn Euler.
DESCRIPCIÓN DE CONJUNTOS
Existen dos formas de describir a los conjuntos por extensión (o tabular o enumeración) y por comprensión (o constructiva o descriptiva).
Cuando el conjunto se describe por extensión se enlistan o nombran a todos los elementos del conjunto, por ejemplo:
El conjunto A de vocales {a, e, i, o, u},
El conjunto B las siete Ss para organizaciones efectivas B = {estructura, estrategia, sistemas, valores comparativos, estilo, habilidades, personal}.
Cuando el conjunto se describe por comprensión consiste en mencionar una regla la cual permite encontrar todos los elementos del conjunto, por ejemplo:
El conjunto A = {x / x sean los números naturales},
El conjunto B = {x / x provincias del Ecuador}.
CLASES DE CONJUNTOS
CONJUNTO FINITO
Un conjunto es finito cuando se pueden contar uno a uno hasta alcanzar el último de los elementos que lo forman, ejemplo.
El conjunto A = {1, 2, 3, 4, 5},
El conjunto B = {x / x sea el número de empleados de un supermercado}.
CONJUNTO INFINITO
El conjunto es infinito si no se conoce el último elemento que lo forma (porque siempre hay un elemento más que contar), ejemplo.
El conjunto A se enlistan algunos de los números primos A = {1, 2, 3, 5, 7, 11, 13,...},
El conjunto B = {x / x sea el número de personas que compran diferentes artículos por Internet}.
CONJUNTO VACÍO O NULO
Es el conjunto que no contiene elementos y se acostumbra representarlo con los símbolos { } o por φ , ejemplo:
- A = {x / x sean las mujeres ecuatorianas que hayan viajado a la luna}
- B = {x / sean las mujeres investigadoras de 100 años de edad en la Antártida}
Muchas veces se define un conjunto vacío recurriendo a un par de contradicciones mutuamente contradictorias, por ejemplo:
A = {x / x > 10 y x < 7} el conjunto A lo llamamos conjunto vacío, por no tener ningún elemento que simultáneamente sea mayor de 10 y menor de 7.
Advertencia:
a) φ es distinto de cero (φ ≠ 0) y de {0}, porque φ es un conjunto sin elementos y {0} es un conjunto con el elemento 0 (cero).
b) El número cero no es un conjunto ( 0 ≠{0} ).
El conjunto vacío φ es un subconjunto de cualquier conjunto A, excepto de sí mismo.
CONJUNTO UNITARIO
Es aquel que tiene uno y sólo un elemento, por ejemplo

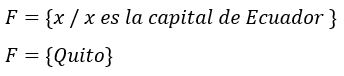
CONJUNTOS IGUALES
Un conjunto "A“ es igual a un conjunto “B", si es que ambos conjuntos tienen los mismos elementos es decir.
Ejemplo.
A = {2, 4 , 6}
B = {6, 4 , 2}
A = B
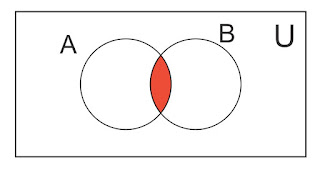
Son aquellos conjuntos, que no tienen ningún elemento común.
Ejemplo.
Sean los conjuntos: A = {2,4, 6, 8}; B = {1, 3, 5, 7, 9} ; A y B son disjuntos; pues no tienen ningún elemento en común. Usando los Diagramas de Venn - Euler, se tiene
CONJUNTO UNIVERSAL (U)
Es el conjunto que contiene, comprende ó dentro del cual están todos los demás conjuntos; se le simboliza por la letra U y gráficamente se le representa mediante un rectángulo en cuyo vértice (uno cualquiera) se coloca la letra U.
El conjunto de libros de una biblioteca, puede ser un ejemplo de conjunto Universal, sus elementos serán cada uno de los libros de los que consta. El marco de referencia es relativo, de modo que podemos referir como Conjunto Universal por ejemplo al conjunto de bibliotecas de la ciudad.
Ejemplo.
sea el conjunto A = {perro, gallina, lagarto, mariposa}
Su universo o conjunto universal será:
U = {Todos los seres animales}
1) DIAGRAMA DE VENN - EULER
Consiste en representar el Conjunto Universal mediante un rectángulo y los otros conjuntos mediante círculos, triángulos o cualquier figura plana.
Ejemplo.
Representar gráficamente.
Gráficamente
2) DIAGRAMAS LINEALES
Sirven para representar las relaciones de Inclusión de 2 ó más conjuntos. Se representa por medio de segmentos verticales.
Ejemplo
A = {1, 3, 5, 7, 9}
B = {3, 7}
B está incluido en A
Al analizar el diagrama lineal tendremos.
Si se tiene el gráfico representar linealmente.
Su representación lineal será.



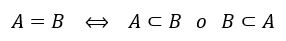










No hay comentarios.:
Publicar un comentario