DEFINICIÓN.
Determinante es el desarrollo de una “matriz cuadrada”. Se le representa simbólicamente encerrando la matriz entre dos barras verticales. El “orden” del determinante está expresado por el número de “filas” o “columnas” que tiene la matriz.
La “matriz es cuadrada” cuando el número de filas es igual al número de columnas.
SIGNOS DE UN ELEMENTO
Se obtiene sumando los números ordinales que indican la fila y columna del elemento.
1) Si la suma es par el elemento tiene signo (+).
2) Si es impar tiene signo (-).
Ejemplo:
Sea el determinante:
El elemento $c_{2}$ se encuentra en 3ra. (3) fila y 2da. (2) columna, luego:
S = 3 + 2 = 5 (número impar)
luego, el elemento $c_{2}$ tiene signo negativo (-).
El elemento $a_{3}$ se encuentra en la 1ra. (1) fila y 3ra. (3) columna, luego:
S = 1 + 3 = 4 (número par)
luego el elemento $a_{3}$ tiene signo positivo (+).
DETERMINANTE DE SEGUNDO ORDEN
Es el desarrollo de una matriz cuadrada que tiene 2 filas y 2 columnas. Se le representa así:
donde $"\bigtriangleup"$ es el valor del determinante.
Los elementos son $a_{1},\, a_{2},\, b_{1},\, b_{2}$
Columnas. Son el grupo de elementos en línea vertical: $\left ( a_{1},\, b_{1} \right )\, y\, \left ( a_{2},\, b_{2} \right )$
Filas. Son el grupo de elementos en línea horizontal: $\left ( a_{1},\, a_{2} \right )\, y\, \left ( b_{1},\, b_{2} \right )$
Diagonal Principal. Está formada por los elementos que van desde el primer elemento de la primera fila al último de la segunda fila. Así:
VALOR DEL DETERMINANTE DE SEGUNDO ORDEN
Es igual al producto de los elementos de la diagonal principal menos el producto de los elementos de la diagonal secundaria.
Ejemplo.
Hallar:
$\bigtriangleup$ = (-5)(4) - (6)(-7)
$\bigtriangleup$ = -20 + 42
$\bigtriangleup$ = 22
DETERMINANTE DE TERCER ORDEN
Es el desarrollo de una matriz cuadrada de 3 filas y 3 columnas.
Para determinar su valor se utiliza la “Regla de Sarrus” o el método de “Menores Complementarios”, que es más general.
REGLA DE SARRUS
1) Se repite las filas primera y segunda a continuación de la tercera (formando 2 filas adicionales).
2) Se toma con signo positivo la diagonal principal (hacia abajo) y las dos paralelas a ella; y con signo negativo, la diagonal secundaria (hacia arriba) y las dos paralelas a la misma.
3) Se efectúan los productos de los elementos de las diagonales y sus paralelas considerando para cada producto el signo señalado en el paso anterior.
Así:
$\bigtriangleup$= $a_{1}b_{2}c_{3}+b_{1}c_{2}a_{3}+c_{1}a_{2}b_{3}-c_{1}b_{2}a_{3}-a_{1}c_{2}b_{3}-b_{1}a_{2}c_{3}$
Ejemplo.
Hallar:
$\bigtriangleup$ = (1)(5)(9) + (2)(6)(7) + (4)(8)(3) - (3)(5)(7) - (6)(8)(1) - (2)(4)(9)
$\bigtriangleup$ = 45 + 84 + 96 - 105 - 48 - 72
$\bigtriangleup$ = 0
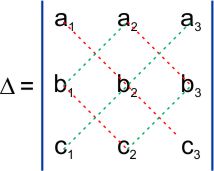
FORMA PRÁCTICA DE LA REGLA DE SARRUS
Cuando se quiere evitar escribir las dos primeras filas a continuación de la tercera, se efectúa los productos de la siguiente manera: como se señala gráficamente.
Desarrollar:
D = $a_{1}b_{2}c_{3}+b_{1}c_{2}a_{3}+a_{2}b_{3}c_{1}-c_{1}b_{2}a_{3}-b_{1}a_{2}c_{3}-c_{2}b_{3}a_{1}$
Ejemplo numérico
Desarrollar:
$\bigtriangleup$ = (3)(16)(1) + (2)(9)(1) + (1)(4)(4) - (4)(3)(1) - (2)(1)(16) - (4)(9)(1)
$\bigtriangleup$ = 48 + 18 + 16 - 12 - 32 - 36
$\bigtriangleup$ = 1
MENOR COMPLEMENTARIO DE UN DETERMINANTE
El menor complementario de un elemento en un determinante, es otro determinante de menor orden, que resulta después de suprimir en el determinante, los elementos que pertenecen a la fila y columna de dicho elemento.
Ejemplo.- Dado el determinante:
es el menor complementario de $b_{2}$.
DESARROLLO DE UN DETERMINANTE POR MENORES COMPLEMENTARIOS
El valor de un determinante es igual a la suma algebraica de los elementos de una línea cualquiera (fila o columna), multiplicado cada uno de ellos por sus respectivos menores complementarios, colocando a cada producto el signo del elemento.
Desarrollar.
desarrollando por los elementos de la 1ra. fila:
$\bigtriangleup$ =$a_{1}\left ( b_{2}c_{3} -c_{2}b_{3}\right )-a_{2}\left ( b_{1}c_{3}-c_{1}b_{3} \right )+a_{3}\left ( b_{1}c_{2}-b_{2}c_{1} \right )$
$\bigtriangleup$ =$a_{1}b_{2}c_{3}-a_{1}c_{2}b_{3}-a_{2}b_{1}c_{3}+a_{2}c_{1}b_{3}+a_{3}b_{1}c_{2}-a_{3}b_{2}c_{1}$
$\bigtriangleup$ =$a_{1}b_{2}c_{3}+a_{2}c_{1}b_{3}+a_{3}b_{1}c_{2}-a_{1}c_{2}b_{3}-a_{2}b_{1}c_{3}-a_{3}b_{2}c_{1}$
Ejemplo.
Desarrollar por menores complementarios:
Solución:
Tomando la primera fila:
$\bigtriangleup$ = (1)(100 - 80) - (4)(75 - 45) + (2)(48 - 36)
$\bigtriangleup$ = 20 - 120 + 24 = -76
PROPIEDADES DE LOS DETERMINANTES
1) Si en un determinante se cambian las filas por columnas y las columnas por filas, el valor del determinante no se altera.
Ejemplo:
2) Si en un determinante se intercambian entre sí dos filas o dos columnas, el determinante cambia de signo.
Ejemplo:
intercambiando las dos filas:
$\bigtriangleup$ = $b_{1}a_{2} - a_{1}b_{2}$
$\bigtriangleup$ = $-\left ( a_{1}b_{2}-a_{2}b_{1} \right )$
$\bigtriangleup$ = $- \Delta _{1}$
3) Si un determinante tiene 2 filas o 2 columnas iguales, el determinante es igual a cero.
Ejemplo:
reduciendo: $\bigtriangleup$ = 0
4) Si en un determinante se multiplica o divide todos los elementos de una fila o columna por un mismo número, el determinante quedará multiplicado o dividido por este número.
Ejemplo:
$\bigtriangleup$ = $a_{1}b_{2}c_{3} + b_{1}c_{2}a_{3} + a_{2}b_{3}c_{1} - c_{1}b_{2}a_{3} - c_{2}b_{3}a_{1} - b_{1}a_{2}c_{3}$
Multiplicando todos los elementos de la primera columna por “m”
OBSERVACIÓN IMPORTANTE
Si un determinante tiene en todos los elementos de una fila o columna un factor común, éste se puede sacar como factor común del determinante.
5) Si todos los elementos de la fila son nulos, el determinante es nulo.
6) Si un determinante tiene dos filas cuyos elementos correspondientes son proporcionales, el determinante es nulo.
7) Si en un determinante a los elementos de una fila o columna se les aumenta o se les resta los de la otra fila o columna paralela multiplicados por un mismo número, el valor del determinante no varía.
Ejemplo:
Sea el determinante:
$\bigtriangleup$ = $a_{1}b_{2} - a_{2}b_{1}$
Multiplicando la primera fila por “m” y sumándole el resultado a la segunda fila, se obtiene:
$\bigtriangleup_{1}$ = $a_{1}(b_{2} + ma_{2}) - a_{2}(b_{1} + ma_{1})$
$\bigtriangleup_{1}$ = $a_{1}b_{2} + ma_{1}a_{2} - a_{2}b_{1} - ma_{2}a_{1}$
$\bigtriangleup_{1}$ = $a_{1}b_{2} + a_{2}b_{1}$
$\therefore \, \, \bigtriangleup$ = $\bigtriangleup_{1}$
EJERCICIOS
Calcular “x” en:
Solución:
Desarrollando el determinante:
4x - 6 + 8 +x + 16 + 12 = 5
5x = 5 + 6 - 8 - 16 - 12
de donde:
x = -5
Calcular el valor de:
Solución:
Aplicando las propiedades establecidas, sumemos a la primera fila, la segunda fila (la única fila que se altera es aquella fila a la cual se suma, permaneciendo las otras iguales).
factorizando el signo en cada uno de los elementos de la primera fila:
factorizando (-1) en el determinante, por la propiedad (4):
El valor del determinante es
E = (-1)(0) = 0
Hallar el valor de:
Solución:
Sacando $a^{p}$ de la 3ra fila:
por tener el determinante la 2da. y 3ra. fila iguales el valor del determinante es cero.
$\Delta$ = $a^{p}$(0) = 0
Calcular el valor de:
Solución:
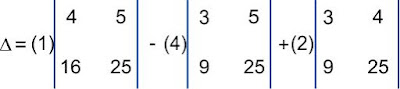
Aplicando el desarrollo por menores complementarios con respecto a la primera fila. Tomando cada elemento con su respectivo signo:
desarrollando los determinantes de tercer orden:
E = (1)(105 + 120 + 120 - 125 - 108 - 112) - (2)(70 + 90 + 96 - 100 - 72 - 84) + (3)(56 + 75 + 72 - 80 - 63 - 60) - 4 (48 + 60 + 60 - 64 - 54 - 50)
E = (1)(0) - 2(0) + 3(0) - 4(0) = 0
E = 0
MÉTODO DE LOS DETERMINANTES PARA HALLAR LA SOLUCIÓN DE UN SISTEMA DE ECUACIONES
Este método permite emplear los determinantes para la resolución de sistemas de ecuaciones mediante la “Regla de Cramer”.
REGLA DE CRAMER
En todo sistema de ecuaciones (determinado), el valor de cada incógnita es una fracción, cuyo denominador es el determinante del sistema, siendo el numerador este mismo determinante en el que se ha reemplazado la columna de los coeficientes de la incógnita por los términos independientes.
EXPLICACIÓN
En el sistema:
$$a_{1}x + a_{2}y = a_{3} \,\,\,(I)$$
$$b_{1}x + b_{2}y = b_{3}\, \,\,(II)$$
se define:
$\Delta s$ = determinante del sistema
$\Delta y$ = determinante de la incógnita y
Por la Regla de Cramer:
$x=\frac{\Delta x}{\Delta s}$
$y=\frac{\Delta y}{\Delta s}$
DISCUSIÓN DE LA SOLUCIÓN DE LOS SISTEMAS LINEALES
Dado el sistema:
$$a_{1}x + a_{2}y = a_{3} \,\,\,(I)$$
$$b_{1}x + b_{2}y = b_{3}\, \,\,(II)$$
Por la Regla de Cramer:
$$x=\frac{\Delta x}{\Delta s}\, \, \, ;\, \, \, y=\frac{\Delta y}{\Delta s}$$
1) Si $\Delta x\neq 0$, $\Delta s\neq 0$, es compatible determinado, tiene una sola solución.
2) Si $\Delta x = 0$, $\Delta s=0$, el sistema es indeterminado, tiene muchas soluciones.
3) Si $\Delta x=0$, $\Delta s\neq 0$, el sistema es incompatible, no tiene solución.
EJERCICIOS
Resolver el sistema:
x + y + z = 0 (1)
ax + by + cz = 0 (2)
bcx + acy + abz = 1 (3)
Solución:
Cálculo de cada determinante:
∆s = $ab^{2} + a^{2}c + bc^{2} - b^{2}c - ac^{2} - a^{2}b$
factorizando por agrupación:
∆s = $b^{2}(a - c) + ac(a - c) - b(a + c)(a - c)$
∆s = $(a - c)(b^{2} + ac - ab - bc)$
∆s = $(a - c)[b(b - a) - c(b - a)]$
∆s = $(a - c)(b - a)(b - c)$
∆x = 0 + 0 + c - (b + 0 + 0)
∆x = c - b
∆y = 0 + a + 0 - (0 + c + 0)
∆y = a - c∆z = b + 0 + 0 - (0 + a + 0)
∆z = b - a$x=\frac{\Delta x}{\Delta s}=\frac{ c-b }{\left ( a-c \right )\left ( b-a \right )\left ( b-c \right )}$
$x=\frac{-\left ( c-b \right )}{\left ( a-c \right )\left ( b-a \right )\left ( b-c \right )}$
$x=-\frac{1}{\left ( a-c \right )\left ( b-a \right )}$
$y=\frac{\Delta y}{\Delta s}=\frac{a-c}{\left ( a-c \right )\left ( b-a \right )\left ( b-c \right )}$
$y=\frac{1}{\left ( b-a \right )\left ( b-c \right )}$
$z=\frac{\Delta z}{\Delta s}=\frac{b-a}{\left ( a-c \right )\left ( b-a \right )\left ( b-c \right )}$
$z=\frac{1}{\left ( a-c \right )\left ( b-c \right )}$
Resolver el sistema:
$$x + y + z = 1\,\,\,(1)$$
$$ax + by + cz = d\,\,\,(2)$$
$$a^{2}x + b^{2}y + c^{2}z = d^{2}\,\,\,(3)$$
Solución:
Al construir los determinantes se nota que son determinantes de Vandermonde.
Para resolver esta matriz debemos hacer ceros en fila 2 en a y la fila 3 en $a^{2}$
Para hacer cero en a y en $a^{2}$ debemos realizar lo siguiente:
f1 (-a) + f2
f1 (-$a^{2}$) + f3
$\Delta s$ = (b - a)(c - a)[(c + a) - (b + a)]
$\Delta s$= (b - a)(c - a)[c + a - b - a]
$\Delta s$ = (b - a)(c - a)(c - b)
entonces el determinante de la matriz
$\Delta s$ = (c - a)(c - b)(b - a)
Luego calculamos los ∆x, ∆y y ∆z utilizando el procedimiento anterior y se obtendrá los siguientes resultados:
$\Delta x$ = (c - d)(c - b)(b - d)
$\Delta y$= (c - a)(c - d)(d - a)
$\Delta z$ = (d - a)(d - b)(b - a)
Para el cálculo de x, y y z se utilizara la Regla de Cramer:
$x=\frac{\Delta x}{\Delta s}=\frac{\left ( c-d \right )\left ( c-b \right )\left ( b-d \right )}{\left ( c-a \right )\left ( c-b \right )\left ( b-a \right )}$
$x=\frac{\left ( c-d \right )\left ( b-d \right )}{\left ( c-a \right )\left ( b-d \right )}$
$y=\frac{\Delta y}{\Delta s}=\frac{\left ( c-a \right )\left ( c-d \right )\left ( d-a \right )}{\left ( c-a \right )\left ( c-b \right )\left ( b-a \right )}$
$y=\frac{\left ( c-d \right )\left ( d-a \right )}{\left ( c-b \right )\left ( b-a \right )}$
$z=\frac{\Delta z}{\Delta s}=\frac{\left ( d-a \right )\left ( d-b \right )\left ( b-a \right )}{\left ( c-a \right )\left ( c-b \right )\left ( b-a \right )}$
$z=\frac{\left ( d-a \right )\left ( d-b \right )}{\left ( c-a \right )\left ( c-b \right )}$
Hallar el valor de “k” si el sistema:
(1 + 2k)x + 5y = 7 (1)
(2 + k)x + 4y = 8 (2)
no tiene solución.
Solución:
Para que el sistema no tenga solución:
$\Delta s$ = 0
El desarrollo del determinante se igual a cero:
4(1+2k) - 5(2+k) = 0
4 + 8k - 10 - 5k = 0
3k = 6
k = 2





































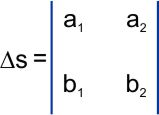

















No hay comentarios.:
Publicar un comentario