INTRODUCCIÓN
La lógica estudia la forma de razonamiento. Es una disciplina que se utiliza para determinar si un argumento es válido, tiene aplicación en todos los campos del saber; en la filosofía, para determinar si un razonamiento es válido o no, ya que una frase puede tener diferentes interpretaciones; sin embargo la lógica permite saber el significado correcto. Los matemáticos usan la lógica, para demostrar teoremas e inferir resultados que puedan ser aplicados en investigaciones.
En la computación, para revisar programas y crear sus algoritmos, es utilizada en el diseño de computadoras. Existen circuitos integrados que realizan operaciones lógicas con los bits, gracias a estos se ha desarrollado las telecomunicaciones (telefonía móvil, internet, ...)
DEFINICIONES BÁSICAS
Término: Cada parte que constituye un enunciado o discurso. Sinónimo de palabra o colección de palabras.
Término categoremático: Término que tiene significado propio e independiente.
Término sincategoremático: Término que no tiene significado propio y se utiliza para modificar o enlazar términos categoremáticos.
Proposición lógica: Agrupación de términos de la que se puede afirmar si su contenido es falso o verdadero. Pueden ser atómicas o moleculares.
Proposición atómica: Proposición que no puede descomponerse en partes que sean a su vez proposiciones.
Proposición molecular: Proposición formada por una o varias proposiciones atómicas enlazadas por términos sincategoremáticos.
Conectores proposicionales: Términos sincategoremáticos que se usan para modificar o enlazar proposiciones.
Conectores monádicos: Se aplican a una sola proposición ej: negación.
Conectores diádicos: Se aplican a dos proposiciones.
Ejemplo: conjunción (y), disyunción (o), disyunción exclusiva (o…o…), condicional (si…entonces), bicondicional (si y solo si).
Simbolizaciones: Proposiciones atómicas se simbolizan por letras minúsculas comenzando por la p : p. q, r, s.
Variable proposicional: Símbolo que sustituye a una proposición atómica.
Conectivo u operador lógico: símbolo del conector proposicional.
Fórmula lógica: Expresión simbólica que sustituye a una proposición molecular.
Valorar o hallar valor lógico de una proposición: averiguar la falsedad o veracidad de la misma. $V\Leftrightarrow verdad\Leftrightarrow 1,F\Leftrightarrow falso\Leftrightarrow 0$
Álgebra de proposiciones: Construcción de fórmulas lógicas y estudio de su veracidad o falsedad así como de sus propiedades.
AXIOMAS DEL ÁLGEBRA DE PROPOSICIONES
Axioma 1: Toda proposición es verdadera o falsa, es decir, toma valores 1 o 0.
Axioma 2: Una fórmula lógica representa una proposición cuyo valor de verdad o falsedad depende de los conectores y los valores de verdad o falsedad de las variables proposicionales que la contienen.
Axioma 3: Los valores de verdad o falsedad de las fórmulas lógicas se establecen en tablas llamadas Tablas de verdad.
Operación lógica: Cuando modificamos o enlazamos una o varias proposiciones mediante conectores obteniendo una nueva proposición.
TABLAS DE VERDAD
Representación de todas las combinaciones posibles de falsedad o veracidad de una proposición atómica o molecular. Contiene $2^{n}$ filas, siendo n la cantidad de variables de la proposición molecular.
Ejemplos de tablas de verdad:
n=1
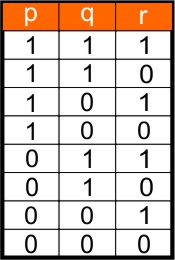
n=3
n=4
OPERADORES LÓGICOS
La validez de una proposición compuesta depende de los valores de verdad de las proposiciones simples que la componen y se determina mediante una tabla de verdad.
Negación: Afecta a una sola proposición. Es un operador monádico que cambia el valor de verdad de una proposición: Dada una proposición p su contraria no p es verdadera cuando aquella es falsa y se simboliza $\sim p$.
Conjunción o producto lógico: Vincula dos proposiciones mediante el conectivo lógico "y". Dadas dos proposiciones p, q , el producto lógico es la proposición molecular p y q que se simboliza $\left ( p\wedge q \right )$.
Disyunción exclusiva: Vincula dos proposiciones mediante el conectivo lógico: "o ..........., o ............." Dadas dos proposiciones p, q , la disyunción exclusiva es la proposición molecular que se simboliza $\left ( p\bigtriangleup q \right )$.
Condicional: Vincula dos proposiciones mediante el conectivo lógico : "Si ............, entonces .............." Dadas dos proposiciones p, q , el condicional es la proposición molecular si p entonces q que se simboliza $\left ( p\rightarrow q \right )$.
Bicondicional: Vincula dos proposiciones mediante el conectivo lógico: ".............. si y sólo si .............." Dadas dos proposiciones p, q , el bicondicional es la proposición molecular p si y solo si q que se simboliza $\left ( p\leftrightarrow q \right )$
IMPORTANTE:
- Cuando los valores del operador principal son todos verdaderos se dice que el esquema molecular es tautológico.
- Se dirá que el esquema molecular es contradictorio si los valores del operador principal son todos falsos.
- Si los valores del operador principal tiene por lo menos una verdad y una falsedad se dice que es contingente o consistente.
LEYES DE ÁLGEBRA PROPOSICIONAL
Son equivalencias lógicas que nos permiten reducir esquemas moleculares complejos y expresarlos en forma más sencilla. Las demostraciones de dichas leyes se hacen construyendo la tabla de verdad en cada caso.
Principales Leyes:
Ley de Idempotencia:
$$p\vee p\equiv p$$
$$p\wedge p\equiv p$$
Ley Conmutativa:
$$p\vee q\equiv q\vee p$$
$$p\wedge q\equiv q\wedge p$$
Ley Asociativa:
$$(p\vee q)\vee r\equiv p\vee (q\vee r)$$
$$(p\wedge q)\wedge r\equiv p\wedge (q\wedge r)$$
Ley Distributiva:
$$p\vee (q\wedge r)\equiv (p\vee q)\wedge (p\vee r)$$
$$p\wedge (q\vee r)\equiv (p\wedge q)\vee (p\wedge r)$$
Ley de la Doble Negación:
$$\sim (\sim p)\equiv p$$
Leyes de Identidad:
$$p\vee V\equiv V\, \, \, ;\, \, \, p\vee F\equiv p$$
$$p\wedge V\equiv p\, \, \, ;\, \, \, p\wedge F\equiv F$$
Leyes del Complemento:
$$p \, \vee \sim p\equiv V$$
$$p \, \wedge \sim p\equiv F$$
Ley del Condicional:
$$p \rightarrow q\equiv \sim p\vee q$$
Ley de la Bicondicional:
$$p \leftrightarrow q\equiv (p\rightarrow q)\wedge (q\rightarrow p)$$
$$p \leftrightarrow q\equiv (p\wedge q)\vee (\sim p \, \wedge \sim q)$$
$$p \leftrightarrow q\equiv \, \sim (p\bigtriangleup q)$$
Ley de Absorción:
$$p \vee (p\wedge q) \equiv \, p$$
$$p \wedge (p\vee q) \equiv \, p$$
$$p\vee (\sim p\wedge q) \equiv \, p\vee q$$
$$p\wedge (\sim p\vee q) \equiv \, p\wedge q$$
Leyes de "De Morgan":
$$\sim (p\vee q) \equiv \, \sim p\, \wedge \sim q$$
$$\sim (p\wedge q) \equiv \, \sim p\,\vee \sim q$$
CUANTIFICADORES:
Cuantificador Universal: Sea la función proposicional $f_{(x)}$ sobre un conjunto A, el cuantificador $\forall$ ("para todo") indica que todos los valores del conjunto A hacen que la función proposicional $f_{(x)}$ sea verdadera.
$\forall$ se lee : "Para todo"
Ejemplo:
Sea : $f_{(x)}:x^{3}+2>5$ donde x$\in $ N
La proposición cuantificada es :
$\forall$ x $\in$ N; $x^{3}+2>5$ es falsa
Cuantificador Existencial: Sea $f_{(x)}$ una función proposicional sobre un conjunto A el cuantificador $\exists $ (existe algún) indica que para algún valor del conjunto A, la función proposicional $f_{(x)}$ es verdadera.
$\exists $ se lee: "Existe algún"
Ejemplo: Sea $f_{(x)}:x^{2}-5<8$, donde: $x\in Z^{+}$, la proposición:
$\exists \, x\in Z^{+}/x^{2}-5<8$ es verdadera.
CIRCUITOS LÓGICOS
Un circuito conmutador puede estar solamente en dos estados estables : cerrado o abierto, así como una proposición puede ser verdadera o falsa, entonces podemos representar una proposición utilizando un circuito lógico:
Circuito Serie: Dos interruptores conectados en serie representan una conjunción.
Circuito Paralelo: Dos interruptores conectados en paralelo representan una disyunción.
LÓGICA BINARIA
La lógica binaria trata con variables que toman 2 valores discretos y con operaciones que asumen significado lógico, para este propósito es conveniente asignar los valores de 1 y 0.
PRINCIPALES COMPUERTAS LÓGICAS
Compuerta AND de dos entradas.
Compuerta OR de dos entradas
Compuerta NOT
Compuerta NAND de dos entradas
Compuerta NOR de dos entradas











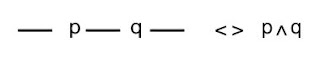





No hay comentarios.:
Publicar un comentario