LONGITUD DE ARCO

Una de las muchas aplicaciones de radián unidad angular es el cálculo de longitud de arco. Sea "l" el arco de una circunferencia de radio "r" interceptado por un ángulo "$\theta$"  radianes.

Si el ángulo AOB mide 1 radián, el arco AB tiene longitud "r", remplazando estos valores el "l"; obtenemos: 

$$ \frac{\angle \, DOC}{\angle \, ABO}=\frac{DC}{AB}$$

$$\frac{\theta\, rad}{1\, rad}=\frac{|}{r}$$ 

De donde: l = r $\cdot \, \, \theta$    ;    $\theta$  en radianes

Siendo: l : longitud de arco
            r : radio de la circunferencia
            $\theta$ : ángulo central expresado en radianes

SECTOR CIRCULAR

Es una parte del circulo como se muestra en la figura, donde el área achurada (sombreada) es el sector circular.

POR GEOMETRÍA

Área Sector Circular = $\frac{\pi r^{2}\theta^{\circ}}{360^{\circ}}$ 
S = $\frac{\pi r^{2}\theta^{\circ}}{360^{\circ}}$    "$\theta$" en grados sexagesimales

POR GEOMETRÍA

Área Sector Circular = $\frac{\pi r^{2}\theta}{360^{\circ}}=\frac{\pi r^{2}\theta}{2\pi }$
S = $\frac{1}{2}r^{2}\theta$    "$\theta$" en radianes

Esta última expresión se puede escribir así: S = $\frac{1}{2}\, \, r\, \, \, \, \, \theta\, \, \cdot \, \, r$        (I)

Por fórmula de longitud de arco:    $\Rightarrow $    $l=\theta\, r$        (II)

Remplazamos (II) en (I)        $\Rightarrow $    S = $\frac{1}{2}l\cdot r$        (III)

De la ecuación (II), despejamos "r": $l=\theta\, r$ $\Rightarrow $ $r=\frac{l}{\theta}$        (IV)

Remplazamos (IV) en (III) 

S = $\frac{l^{2}}{2\, \theta}$        (Fórmula)

Ejercicios:

1) Dada la circunferencia de 24 m de radio. Encontrar la longitud de arco subtendido por el ángulo central de 2/3 radianes.

Resolución:

Por fórmula:

$L_{\widehat{AB}}=\angle \, rad\times radio$

Remplazamos los valores y obtenemos:

$L_{\widehat{AB}}=\frac{2}{3}\times 24\, m=2\times 8\, m$
$L_{\widehat{AB}}=16\, m$

2) Encontrar el radio de una circunferencia tal que un arco de 15 m de longitud. Subtiende un ángulo central de 3 rad.

Resolución:

$L_{\widehat{AB}}=\angle \, rad\times radio$

Remplazamos los valores y obtenemos:

15 m = 3 x r
r = $\frac{15\, m}{3}$
r = 5 m

3) La figura es un semicírculo. Hallar: $L_{1}+L_{2}-L_{3}$

Resolución:

De la figura:

$ \theta+3\theta+2\theta=180^{\circ} $

$6\theta=\pi$ rad
$\theta=\frac{\pi}{6}$ rad

Por fórmula:

$L_{\widehat{AB}}=\angle \, rad\times radio$

Remplazamos los valores y obtenemos:

$L_{1}=2\theta\,  rad\times \pi\,  m$
$L_{1}=2\left ( \frac{\pi }{6} \right )\cdot \pi \, m$
$L_{1}=\left ( \frac{\pi^{2} }{3} \right )\, m$        (I)

Aplicando la misma fórmula

$L_{2}=3\theta\,  rad\times \pi\,  m$
$L_{2}=3\left ( \frac{\pi }{6} \right )\cdot \pi \, m$
$L_{2}=\left ( \frac{\pi^{2} }{2} \right )\, m$        (II)

Aplicando la misma fórmula

$L_{3}=\theta\,  rad\times \pi\,  m$
$L_{3}=\left ( \frac{\pi }{6} \right )\cdot \pi \, m$
$L_{3}=\left ( \frac{\pi^{2} }{6} \right )\, m$        (III)

Luego: $L_{1}$ + $L_{2}$ +$L_{3}$ = $\left ( \frac{\pi^{2} }{3} \right )\, m$ + $\left ( \frac{\pi^{2} }{2} \right )\, m$    + $\left ( \frac{\pi^{2} }{6} \right )\, m$ 

$L_{1}$ + $L_{2}$ +$L_{3}$ = $\left ( \frac{2}{3}\pi ^{2} \right )\, m$

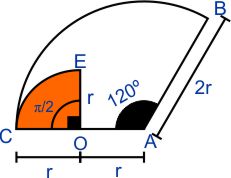
4) Si la longitud del arco $\widehat{BC}$ es 4$\pi$ m y "O" es punto medio de $\overline{AC}$. Calcular el área de la  región sombreada ($\overline{CO}=\overline{OA}=\overline{OE}$)

Resolución:

Convertimos 120º a radianes

120º: 120º x $\frac{\pi\,  rad}{180^{\circ}}=\frac{2}{3}\pi$ rad
120º = $\frac{2}{3}\pi$ rad

Por la fórmula:

$L_{\widehat{BC}}=\theta \, rad\times radio$

Donde:

4$\pi$ m = $\frac{2}{3}\pi$ x (2r)
$2r = \frac{4\pi \, m}{\frac{2}{3}\, \pi}$
$2r = 6\, m$
$r = 3\, m$

Recordar que:

El área del sector circular 

AOB = $\frac{1}{2}\, r^{2} \, \theta$
donde: "$\theta$" en radianes 

Luego: área COE = $\frac{1}{2}\, r^{2} \, \theta$
          área COE = $\frac{1}{2}\, \left ( 3\, m \right )^{2}\times \frac{\pi}{2}$ 
          área COE = $\frac{9}{4}\pi m^{2}$

5) De la siguiente figura. La longitud del arco $\widehat{AB}$es 2$\pi$ m, Calcular el área de la región sombreada ($\overline{AO}=\overline{OB}=\overline{OC}=12$) 

Resolución:

Por fórmula: 

$L_{\widehat{AB}}=\pi\, rad\times radio$

2$\pi$ m = $\theta$ rad x 12 m
$\theta=\frac{\pi}{6}$

De la región: 

$\theta +\beta=90^{\circ}$
$\frac{\pi}{6}$ rad + $\beta$ = $\frac{\pi}{2}$ rad
$\beta$ = $\frac{\pi}{2}$ rad - $\frac{\pi}{6}$ rad

Luego calculamos el área de la región sombreada:

área BOC = $\frac{1}{2}\left ( 12\, m \right )^{2}\times \frac{\pi}{3}$
área BOC = 72 $m^{2}\times \frac{\pi}{3}$
área BOC = 24 $\pi\, m^{2}$

6) Determinar el valor de "L" en el esquema siguiente:

Resolución:

Por fórmula:

$L_{\widehat{AF}}=\theta\, rad\times radio$

Luego: 4 = $\theta$ x r        (I)

Aplicando la misma fórmula:

$L_{\widehat{BE}}=\theta\, \times \left ( r+3 \right )$
L = $\theta\, \times r+3\theta$        (II)

Remplazamos (I) en (II) 

L = 4 +3$\theta$        (III)

Nuevamente aplicamos la misma fórmula:

$L_{\widehat{CD}}=\theta\, \times \left ( r+5 \right )$
14 = $\theta$ x r + 50            (IV)

Remplazamos (I) en (IV) 

14 = 4 + 5$\theta$
10 = 5$\theta$
$\theta$ = 2

Luego, remplazamos $\theta$ = 2; en (III): 

L = 4 +3$\theta$
L = 4 +3(2)
L = 10