FUNCIONES TRIGONOMÉTRICAS EN LA CIRCUNFERENCIA TRIGONOMÉTRICA

CIRCUNFERENCIA TRIGONOMÉTRICA.

Es una circunferencia inscrita en un sistema de coordenadas rectangulares cuyo criterio coincide con el origen de dicho sistema, esta circunferencia tiene como característica fundamental, el valor del radio que es la UNIDAD (R = 1). Esta circunferencia trigonométrica sirve para representar las líneas trigonométricas.

Nota: la ecuación "$x^{2}+y^{2}=1$" es la ecuación Canónica de la circunferencia de R = 1 y centro O (0 , 0)

ELEMENTOS DE LA CIRCUNFERENCIA.

Se tiene los siguientes elementos: 

O (0 , 0): Origen de la circunferencia.

A (1 , 0): Origen de los Arcos, a partir del cual se miden los ángulos trigonométricos es decir ángulos positivos, negativos y de cualquier magnitud.

B (0 , 1): Origen de complementos.   

A' (-1 , 0): Origen de complementos.

B' (0 , -1): Sin denominación especifica, P (x, y): Punto "P" de coordenadas (x , y).    

PROPIEDADES CONVENCIONALES.

a) Radio de la Circunferencia igual a la UNIDAD.

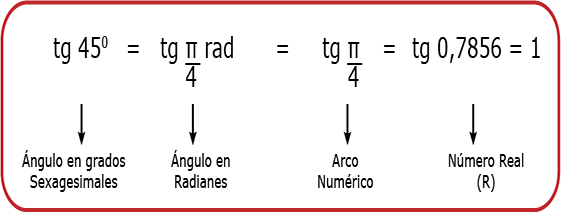
b) Cuatro cuadrantes numerados, cada uno de los cuales mide 90º, 100 g ó $\frac{\pi}{2}$ rad.

c) Se adaptan los signos de los ejes coordenadas o sea los segmentos $\overline{OA}$ y $\overline{OB}$ son positivos y $\overline{OA'}$ y $\overline{OB'}$ son negativos.

Características de la Circunferencia Trigonométrica:

Por la fórmula: 

$\theta=\frac{L}{R}$    ;    R = 1

$\theta=\frac{L}{1}$    $\Rightarrow \,\,\,\, \therefore$ $\theta$ = L    (Sólo se cumple numéricamente)

Es decir que el número de radianes del ángulo central es igual a la longitud de arco pero sólo como arco numérico.

LÍNEAS TRIGONOMÉTRICAS

LÍNEA SENO:

Representación:

Se representa por la perpendicularidad trazada desde el extremo del arco, hacia el diámetro horizontal.

En el triángulo OQP:

sen $\theta$ = $\frac{\overline{PQ}}{\overline{OP}}=\frac{y}{1}$ $ \Rightarrow \; \; \therefore $ sen $\theta$ = y

De la figura: sen $\widehat{AP}$ = sen $\theta$ = $\overline{PQ}$ = y   

LÍNEA COSENO:

Representación:

Se representa por la perpendicularidad trazada desde el extremo del arco, hacia el diámetro vertical:

En el triángulo PNO:

cos $\theta$ = $\frac{\overline{PN}}{\overline{OP}}=\frac{x}{1}$ $ \Rightarrow \; \; \therefore $ cos $\theta$ = x

De la figura: cos $\widehat{AP}$ = cos $\theta$ = $\overline{NP}$ = x   

LÍNEA TANGENTE:

Representación:

Es una parte de la tangente geométrica trazada por el origen de arcos A (1 , 0), se empieza a medir de este origen y termina en la intersección de la tangente geométrica con el radio prolongado que pasa por el extremo del arco. 

En el triángulo TAO:

tg $\theta$ = $\frac{\overline{AT}}{\overline{OA}}=\frac{y_{1}}{1}$ $ \Rightarrow \; \; \therefore $ tg $\theta$ = $y_{1}$

De la figura: tg $\widehat{AP}$ = tg $\theta$ = $\overline{AT}$ = $y_{1}$    

LÍNEA COTANGENTE:

Representación:

Es una parte de la tangente que pasa por el origen de complementos B (0 , 1), se empieza a medir de ese origen y termina en la intersección de la tangente mencionado con radio prolongado que pasa por el extremo del arco.

En el triángulo TBO:

cotg $\theta$ = $\frac{\overline{BT}}{\overline{BO}}=\frac{x_{1}}{1}$ $ \Rightarrow \; \; \therefore $ cotg $\theta$ = $x_{1}$

De la figura: cotg $\widehat{AP}$ = cotg $\theta$ = $\overline{BT}$ = $x_{1}$  

LÍNEA SECANTE:

Representación:

Es una parte del diámetro prolongado que pasa por el origen del arco, se empieza a medir del centro de la circunferencia y termina en la intersección del diámetro prolongado con la tangente geométrica trazada por el extremo del arco.

En el triángulo OPT:

sec $\theta$ = $\frac{\overline{OT}}{\overline{OP}}=\frac{x_{2}}{1}$ $ \Rightarrow \; \; \therefore $ sec $\theta$ = $x_{2}$

De la figura: sec $\widehat{AP}$ = sec $\theta$ = $\overline{OT}$ = $x_{2}$

LÍNEA COSECANTE:

Representación:

Es una parte del diámetro prolongado que pasa por el origen de complementos, se empieza a medir en el centro de la circunferencia y termina en la intersección del diámetro prolongado con la tangente geométrica trazada por el extremo del arco.

En el triángulo OPT:

cosec $\theta$ = $\frac{\overline{OT}}{\overline{OP}}=\frac{y_{2}}{1}$ $ \Rightarrow \; \; \therefore $ cosec $\theta$ = $y_{2}$

De la figura: cosec $\widehat{AP}$ = cosec $\theta$ = $\overline{OT}$ = $y_{2}$

Otras Líneas Auxiliares en la Circunferencia Trigonométrica

Línea Seno Verso o Verso (Vers):

Es lo que falta al coseno de un arco para valer la unidad.

Es verso se empieza a medir a partir del origen de versos que viene hacer el origen de arcos A (1 , 0), y termina en el pie de la perpendicular trazada desde el extremo del arco al diámetro horizontal. El verso es siempre positivo.

Por definición:

Vers $\theta$ = 1 - cos $\theta$        (I)

De la figura: Vers $\theta$ = MA

En el triángulo OMP: 

cos $\theta$ = $\frac{\overline{OM}}{\overline{OP}}=\frac{\overline{OM}}{1}$ 

cos $\theta$ = $\overline{OM}$        (II)

Remplazamos (II) en (I): 

Vers $\theta$ = 1 - cos $\theta$

$ \Rightarrow \; \; \therefore $ Vers $\theta$ = $\overline{MA}$

Línea Coseno Verso o Converso (COV.):

Es lo que falta al seno de un arco para valer la unidad.

El converso se empieza a medir en el origen de conversos que viene a ser el origen de complemento B (1 , 0); y termina en el pie de la perpendicular trazada desde el extremo del arco al diámetro vertical de la circunferencia trigonométrica. El converso es siempre positivo.

Por definición:

cov $\theta$ = 1 - sen $\theta$        (I)

De la figura: cov $\theta$ = $\overline{BM}$

En el triángulo OMP: 

sen $\theta$ = $\frac{\overline{MO}}{\overline{OP}}=\frac{\overline{OM}}{1}$ 

sen $\theta$ = $\overline{MO}$        (II)

Remplazamos (II) en (I): 

cov $\theta$ = 1 - $\overline{MO}$

$ \Rightarrow \; \; \therefore $ cov $\theta$ = $\overline{MB}$

Línea Ex-Secante o External (Ex-Sec.):

Es el exceso de la secante respecto a la unidad.

La ex-secante se mede a partir del origen de exsecantes que viene a ser el origen de arcos y termina en el punto donde la secante de ese arco.

Si la secante se mide hacia la derecha del origen de exsecantes es positiva y el caso contrario es negativa.

Por definición:

ex-sec $\theta$ = sec $\theta$ - 1        (I)

De la figura: ex-sec $\theta$ = $\overline{AQ}$

En el triángulo OPQ: 

sec $\theta$ = $\frac{\overline{OQ}}{\overline{OP}}=\frac{\overline{OQ}}{1}$ 

sec $\theta$ = $\overline{OQ}$        (II)

Remplazamos (II) en (I): 

ex-sec $\theta$ = 1 - $\overline{OQ}$

$ \Rightarrow \; \; \therefore $ ex-sec $\theta$ = $\overline{AQ}$

NOTA: Para la resolución de los problemas hay que tener los siguientes conceptos.

Circunferencia: Línea curva cerrada cuyos puntos están todos a igual distancia de un punto interior llamado centro.

Círculo: Superficie comprendida dentro de la circunferencia.

Ejercicio.

En la circunferencia trigonométrica: $\overline{OS}=\frac{5}{3}$; Hallar: $\overline{BT}$

Resolución.

Sea el $\angle POA=\alpha$ Entonces: $\angle OST=\alpha$ 

En el triángulo SBT:

tg $\alpha$ = $\frac{\overline{BT}}{\overline{SB}}$

$\Rightarrow \;\;\overline{SB}\bullet tg\;\alpha=\overline{BT}$    (I)

De la figura:

$\overline{SB}=\frac{2}{3}$        (II)

Remplazando (II) en (I): $\frac{2}{3}$ . tg $\alpha $ = $\overline{BT}$        (III)

En el triángulo OPS: Aplicamos el teorema de Pitágoras:

$\overline{OS^{2}}=\overline{OP^{2}}+\overline{PS^{2}}$

$\left ( \frac{5}{3} \right )^{2}=1^{2}+\overline{PS^{2}}$

$\frac{25}{9}-1=\overline{PS^{2}}$

$\frac{4}{3}=\overline{PS}$

Además: tg $\alpha $ = $\frac{\overline{OP}}{\overline{PS}}$ = $\frac{1}{\frac{4}{3}}=\frac{3}{4}$

tg $\alpha $ = $\frac{3}{4}$        (IV)

Remplazamos (IV) en (III)

$\frac{2}{3}$ . $\frac{3}{4} $ = $\overline{BT}$

$\overline{BT}$ = $\frac{1}{2} $ = 0,5

Ejercicio.

En la circunferencia trigonometrica de la figura. Calcular: $\overline{AT}\times \overline{OQ}\times \overline{AR}$ $\left ( Si\; \; \overline{PQ}=\overline{QR} \right )$.

Resolución:

De la figura.

$\angle TOA=\angle PTQ=\alpha$ por ser ángulos correspondientes

Por la propiedad: (En el triángulo RTP)

$\angle RTQ=\angle PTQ=\alpha$ por ser un triángulo isósceles.

En el triángulo OAT: tg $\alpha $ = $\frac{\overline{TA}}{\overline{OA}} =\frac{\overline{TA}}{1}$

$\Rightarrow \; \therefore \; \overline{TA}$ = tg $\alpha $

De acuerdo a la figura: $\overline{TA} =\overline{QR}=\overline{PQ}$ = tg $\alpha $

$\Rightarrow \; \overline{PQ}$ = tg $\alpha $

En el triángulo RAT: cotg $\alpha $ = $\frac{\overline{AR}}{TA}=\frac{\overline{AR}}{tg\; \alpha }$

$\Rightarrow \; cotg\; \alpha\; .\; tg\; \alpha =\overline{AR} $

$\Rightarrow \;\therefore \; 1 =\overline{AR}$

Luego: $\overline{AT}\times \overline{PQ} \times \overline{AR}$ = tg $\alpha$ . 1 = $tg^{2}\; \alpha $