RAZONES TRIGONEMÉTRICAS DE UN ÁNGULO DE CUALQUIER MAGNITUD

ESCALA NUMÉRICA.

Una recta dirigida es una recta en la que se han señalado dos sentidos; uno positivo y otro negativo. El sentido se indica con una flecha.

Se determina una escala numérica cuando se escogen un punto "O", llamado origen, y una unidad de medida "OA = 1", es una recta dirigida, en esta escala "B" esta situado a 4 unidades a la derecha de "O" ( esto es en el sentido positivo a partir de "O") y "C" esta a dos unidades a la izquierda de "O" (esto es, en el sentido negativo a partir de "O").

La distancia dirigida "OB = +4" y la distancia dirigida "OC = -2". Es importante observar que puesto que la recta está dirigida, "OB $\neq $ BO" y "OC $\neq $ CO". La distancia dirigida "BO = -4", porque se mide en sentido contrario al que se ha tomado como positivo y la distancia dirigida "CO = +2". Entonces "CB = CO + OB = 2 + 4 = 6" y "BC = BO + OC = (-4) + (-2) = -6.

SISTEMA DE COORDENADAS RECTANGULARES (S.C.R.).

Es un plano que se forma al cortarse perpendicularmente dos rectas, una de las rectas se designa como eje "x" y la otra como "y".

Ejes de Coordenadas:

x'x : Es el eje de las abscisas o eje de las "x".

yy' : Es el eje de las ordenadas o eje de las "y".  

O : Es el origen de coordenadas.

Semi Ejes:

Ox : Es el semieje (+) de las abscisas.

Ox' : Es el semieje (-) de las abscisas.

Oy : Es el semieje (+) de las ordenadas.

Oy' : Es el semieje (-) de las ordenadas.    

Cuadrantes:

El primer cuadrante es xOy : ($Q_{1}$)    

El primer cuadrante es yOx' : ($Q_{2}$)    

El primer cuadrante es x'Oy' : ($Q_{3}$)    

El primer cuadrante es xOy' : ($Q_{4}$)   

Posición de un Punto o Coordenadas de un Punto.

Se llama así a la localización de un punto en un plano cartesiano. Así.

Abscisa de un Punto.

Es la distancia de un punto al eje de las ordenadas.

De la figura: MP = ON    $\Rightarrow $    Abscisa.

Ordenada de un Punto.

Es la distancia de un punto al eje de las abscisas.

De la figura: OM = NP    $\Rightarrow $    Ordenada.

Analíticamente un Punto se representa así:

P ( a , b) donde "a" es la abscisa y "b" la ordenada del punto.

Observación: Al Punto P ( a , b), también se llama "Par Ordenado" de números, es un par en el cual el orden es importante. Así el par ordenado (-3 , 6) no es igual que el par ordenado (6 , -3). Además a , b pertenecen al campo de los números reales.

Determinación de un Punto por sus Coordenadas.

Localice los puntos: A(3, 4); B(-2 , 5); C(-1 , 3); D(0 , 2) y E(6 , 0)

• En primer lugar, se trazan dos rectas dirigidas, perpendiculares entre si.
• En segundo lugar marcamos sobre ellas, unidades de tamaños adecuados.
• El punto "A", tiene abscisa 3 positiva y ordenada 4 positiva.
• El punto "B", tiene abscisa 2 negativa y ordenada 5 positiva.
• El punto "C", tiene abscisa 1 negativa y ordenada 3 positiva.
• El punto "D", tiene abscisa cero y ordenada 2 positiva.
• El punto "E", tiene abscisa 6 positiva y ordenada cero.

Radio Vector (r): Es el segmento dirigido que va del origen al punto P (a , b) y se representa por "r" y es siempre positiva, su valor está dado por la fórmula:

$$r=\sqrt{a^{2}+b^{2}}$$

Demostración:

• Ubicamos el Punto P (a , b), en el plano cartesiano.

• Por el teorema de Pitágoras, calculamos "r".

 $$r^{2}=a^{2}+b^{2}$$

De donde

$$|r|=\sqrt{a^{2}+b^{2}}$$

Siendo:

a = abscisa.

b = ordenada.

r = radio vector, (r > O)

ÁNGULO EN POSICIÓN NORMAL.

Un ángulo está en posición normal si su vértice está en el origen y su lado inicial coincide con el semieje positivo de las abscisas y su lado final en cualquier parte del plano. Si el lado final coincide con un eje, el ángulo es múltiplo de 90º.

$\alpha$ : ángulo en posición normal (+)

$\beta$ : ángulo en posición normal (-)

OA : coincide con el eje (+) Ox

$\alpha$ : ángulo de $Q_{1}$ (Primer Cuadrante)

$\beta$ : ángulo de $Q_{3}$ (Tercer Cuadrante)

Ejemplo:

Trace en posición normal un ángulo cuyo lado terminal pasa por el punto (-3 , -4).

 Resolución:

Según la figura $\theta$ es un ángulo positivo y $\phi$ es un ángulo negativo. Donde los ángulos cumplen con la condición del problema.

ÁNGULOS COTERMINALES.

Dos o más ángulos en posición normal son coterminales cuando sus lados  finales coinciden, si dos ángulos coterminales, su diferencia deben dar; un número entero de vueltas o revoluciones.

a) ÁNGULOS COTERMINALES QUE TIENEN ORIENTACIÓN POSITIVA.

En la figura, $\alpha$ y $\beta$ son coterminales además se observa que:

$\beta$ = 1 vuelta + $\alpha$

Donde: $\beta$ - $\alpha$ = 1 vuelta

En general: si "x" e "y" son coterminales 

x - y = n vueltas        ó        x - y = n revoluciones

Luego: x - y = n rev. = 2 n $\pi$ rad. = n x 360º

b) ÁNGULOS COTERMINALES QUE TIENEN ORIENTACIÓN NEGATIVA. 

En la figura, $-\alpha$ y $-\beta$ son coterminales además se observa que:

$-\beta$ = $-\alpha$ - 360º

Donde: 360º = $\beta$ - $\alpha$ 

En general: si "x" e "y" son coterminales 

Entonces: x - y = n rev. = 2 n $\pi$ rad. = n x 360º

Siendo: "n" número entero.

c) ÁNGULOS CUADRANTALES.

Un ángulo en posición normal, es cuadrantal, cuando su lado final coincide con cualquiera de los semiejes de un sistema de coordenadas rectangulares. Los ángulos cuadrantes no pertenecen a ningún cuadrante y son de la forma: n x 90º ó n x $\frac{1}{2}$ rad. ($\forall$ n $\in $ Z).

Razones Trigonométricas de un Ángulo en Posición Normal.

Las razones trigonométricas de un ángulo $$ se define como se muestra en la tabla: en las definiciones que siguen, se va a establecer como el dominio y el recorrido de las razones trigonométricas aunque deberían ser evidentes.

Sea $\theta$ un ángulo en posición normal y sea "P" un punto cualquiera distinto de O en el lado terminal de $\theta$.

TABLA

Propiedad Fundamental: Las razones de dos o más ángulos coterminales, son iguales.

Ejemplo.

sen 400º ?

Resolución.

$\Rightarrow $    $\therefore$    sen 400º = sen 40º

Ejemplo.

cos 730º ?

Resolución.

$\therefore$    cos 730º = cos 10º

EN GENERAL: Si: $\alpha$ y $\theta$ son coterminales ($\alpha $ > 0), entonces:

Razón trigonométrica $\alpha$ = Razón trigonométrica (n x vueltas + $\theta$) = R.T. ($\theta$) 

R.T. ($\circ $) = R.T. (n x Rev. + $\theta$) = R.T. ($\theta$)

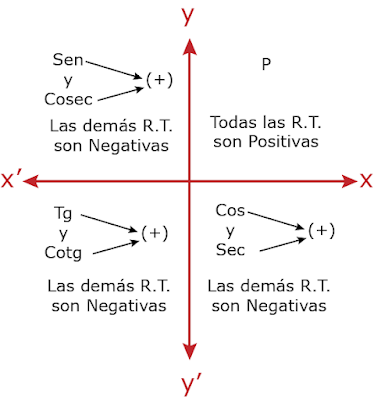
SIGNO DE LAS RAZONES TRIGONOMÉTRICAS

En el presente cuadro se ofrece el signo de cada razón trigonométrica para cada cuadrante.

Siendo:

P: Primer Cuadrante

S: Segundo Cuadrante

T: Tercer Cuadrante

C: Cuarto Cuadrante

R.T.:  Razón Trigonométrica.

VALORES QUE PUEDEN TOMAR LAS RAZONES TRIGONOMÉTRICAS

Ejercicio.

Siendo: Cos $\theta$ = 0, $\widehat{3}$; ($\theta\,\in \,Q_{1}$):

Calcular : "tg $\theta$"

Resolución.

De la condición: cos $\theta$ = 0, $\widehat{3}$ = $\frac{3}{9}$ = $\frac{1}{3}$ 

Graficando:

Por el teorema de Pitágoras:

$\overline{OP^{2}}=\overline{PH^{2}}+\overline{OH^{2}}$

$3^{2}=\overline{PH^{2}}+1^{2}$

9 = $\overline{PH^{2}}$ + 1

8 = $\overline{PH^{2}}$

$\sqrt{8}=\overline{PH}$

$\therefore $    $2\sqrt{2}=\overline{PH}$

Luego: $tg\,\theta=\frac{\overline{PH}}{OH}=\frac{2\sqrt{2}}{1}$

            $tg\,\theta={2\sqrt{2}}$

Ejercicio.

Siendo: sen $\theta$ = 0,96; ($\theta\,\in \,Q_{2}$):

Calcular : E = sec $\theta$ - tg $\theta$

Resolución:

De la condición: sen $\theta$ = 0,96 = $\frac{96}{100}$ = $\frac{24}{25}$ 

Graficando.

Por el teorema de Pitágoras:

$\overline{OP^{2}}=\overline{PH^{2}}+\overline{OH^{2}}$

$25^{2}=24^{2}+\overline{PH^{2}}$

625 =576+ $\overline{PH^{2}}$

49 = $\overline{PH^{2}}$

$\sqrt{49}=\overline{PH}$

7 = $\overline{PH}$

-7 = $\overline{PH}$

Luego: 

E = sec $\theta$ - tg $\theta$

E = $\frac{\overline{OP}}{\overline{OH}}-\frac{\overline{PH}}{\overline{OH}}$ 

E = $\frac{25}{-7}-\frac{24}{-7}$

E = -$\frac{1}{7}$

Ejercicio.

Hallar el equivalente de: sen 1470º

Resolución:

En primer lugar realizamos la siguiente operación 

1470º = 4 X 360º + 30º

Luego: 

Respuesta: sen 1470º = sen 30º = $\frac{1}{2}$